|
Оценка
времени выполнения работ
Вероятная или нормативная продолжительность (для известных работ)
[в количестве дней]
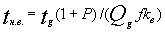 ,
где ,
где
Р- доля дополнительных работ
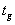 -
трудность работы -
трудность работы
Q-количество работников, участвующих в данной работе
g-число часов в рабочем дне
f-коэффициент перевода рабочих дней в календарные с учетом отпусков (f=0,66)
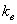 -
коэффициент выполнения норм (1-1,3) -
коэффициент выполнения норм (1-1,3)
Для работ время выполнения, которых неизвестно даются: три или две вероятностные оценки времени.
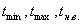 (наиболее вероятные)
(наиболее вероятные)
Эти величины являются исходными для расчета 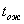
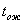 -представляет
собой математическое ожидание случайной величины (в данном случае это
продолжительность работы) -представляет
собой математическое ожидание случайной величины (в данном случае это
продолжительность работы)
Математическое ожидание - дает представление о положении случайной величины (указывает некоторое среднее ориентировочное значение, около которого группируются все возможные значения случайной величины).
Для более полной характеристики распределения случайных величин в теории вероятности используется понятие дисперсии.
Дисперсия (рассеивание)- мера неопределенности, связанная с данным рассеиванием; квадрат отклонения случайной величины от ее математического ожидания.
При большом значении дисперсии – существует значение неопределенность относительно момента завершения данной работы. При малом значении дисперсии ТО имеется большая уверенность, относительно момента завершения данной работы. ТО от значений дисперсии отдельных работ зависит неопределенность срока окончания всего проекта в целом и следственно сведения о дисперсии играют, возможную роль в анализе соответствующего графика.
Т. к. В сетевом планировании продолжительность многих работ рассматривается, как случайная величина, - одной из важнейших проблем при создании аппарата для расчета С. П. является установление характера распределения случайных величин – оценок работ.
Закон распределения считается установленным, если определено соотношение, характеризующее связь между возможными значениями случайных величин и соответствующей им вероятности.
Закон распределения – функция, с помощью которой можно полностью описать случайную величину с вероятностной точки зрения.
Наиболее известным является нормальное или гауссово распределение. В практике установлено, что распределение продолжительности работ обладают положительной асимметрией (т. е. единый max кривой смещен влево относительно линии делящей площадь под кривой на две равных части).
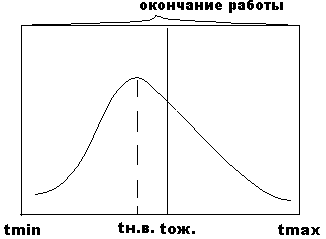
Наиболее подходящими (из всех) являются законы распределения:
Бета - распределения (наиболее популярен), гамма – распределения и логарифмически - нормальный закон.
Бета – распределение – это основное распределение математической статистики для случайных величин, ограниченных с обеих сторон. (Этот закон имеет место, когда случайная величина зависит от большого числа случайных факторов, которые оказывают незначительное влияние и одновременно от некоторых факторов, которая существенно меньше окончательной оценки).
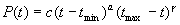 (1), где
(1), где
t - случайная величина, соответствующая времени выполнения работы;
с - коэффициент, определяемый из условия 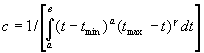 ,
а и ,
а и 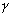 -
параметры распределения. -
параметры распределения.
Существует два основных из возможных вариантов задания распределения.
1. Для каждой работы вводят три оценки
времени: 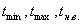 .
Кроме того, принимаются допущения, что дисперсия .
Кроме того, принимаются допущения, что дисперсия 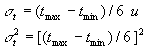
В действительности значения 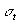 колеблются в интервале от 1/5 до 1/7 интервала
колеблются в интервале от 1/5 до 1/7 интервала 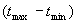 .
При сделанных допущениях математическое ожидание: .
При сделанных допущениях математическое ожидание:
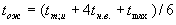 . .
2. Другой вид будет иметь выражение для 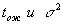 ,
если параметрам а и ,
если параметрам а и 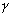 придать фиксированные значения а=1,
придать фиксированные значения а=1, 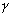 =2. =2.
В этом случае 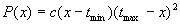 .
Т.к. площадь под кривой распределения равна 1, т. е. .
Т.к. площадь под кривой распределения равна 1, т. е. 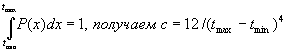 .
Функция плотности распределения записывается в этом .
Функция плотности распределения записывается в этом
случае : 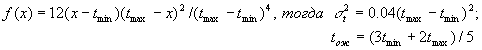
Второй вариант более распространен, т. к. требует меньше данных от экспертов
(только 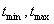 .) .)
Ошибки по этим вариантам менее 1%. Т. О. 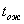 берется либо по справочникам, либо по формулам.
берется либо по справочникам, либо по формулам.
ОСНОВЫ ОПТИМИЗАЦИИ СГ.
Под оптимизацией СГ понимается процесс улучшения организации выполнения комплекта работы с учетом установленного срока и использования ресурсов. Она (СГ) осуществляется:
- За счет перераспределения ресурсов:
- временных (использование резервов времени)
- материальных;
- энергетических;
- рабочей силы.
- За счет интенсификации выполнения работ критического пути:
- дополнительное количество исполнителей;
- оборудование;
- материальное стимулирование.
- За счет параллельного выполнения работ критического пути
- За счет изменений в характере комплекта работ.
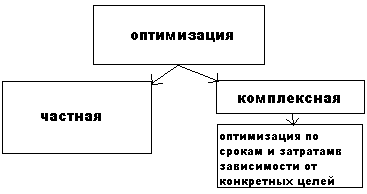 Оптимизация
СГ в зависимости от полноты работ может быть условно разделена на частную
и комплексную. Оптимизация
СГ в зависимости от полноты работ может быть условно разделена на частную
и комплексную.
- Минимизация времени выполнения разработки при заданной ее стоимости (задача 1)
- Минимизация потребляемых (используемых одновременно) ресурсов (задача 2)
- Минимизация стоимости всего комплекса работы при заданном времени выполнения проекта (задача 3)
При минимизации времени выполнения работ (задача 1) (оптимизация по критерию “время”) общий срок выполнения работы следует сокращать в первую очередь за счет изменения продолжительности критических работ. Топология сети при этом не меняется, меняются лишь временные оценки. При этом следует помнить, что уменьшение времени выполнения работ на критическом пути ведет к увеличению “подкритических” путей (что уменьшению на них запаса времени).
Основные источники уменьшения времени критического пути:
а) за счет внутренних резервов;
б) за счет привлечения дополнительных ресурсов.
Внутренние резервы:
- за счет интенсификации выполненных действий;
- за счет лучшей организации труда;
- за счет повышения уровня их механизации и автоматизации.
Дополнительные резервы:
- конечно, более привлекательны для ответственных исполнителей этих работ, чем их интенсификация.
Обычно речь идет не о внешних для проекта в целом источников увеличения ресурсов, а о перераспределении ресурсов, например, работников между работами. Переброска работников некритических работ на критические сопровождается увеличением сроков выполнения некритических работ и сокращением на них резервов. (Резервы времени на них будут сокращаться, как за счет общего уменьшения критического пути, так и за счет увеличения длительности некритических работ).
Маневрирование ресурсами работников и сокращение за счет этого критического пути возможно:
- если специалисты, выполняющие параллельные работы взаимозаменяемы
- если эти группы специалистов подчинены одному руководителю.
Если такие условия не выполнены, то дальнейшая оптимизация может потребовать выделения дополнительных внешних ресурсов.
Следующим этапом оптимизации (пока сокращения критического пути) СГ является минимизация потребности в исполнителях (задача2). Что достигается путем смещения сроков начала (и соответственно окончания) работ подкритических путей.
Наглядно представить процесс изменения резервов времени и потребности в исполнителях на отдельных этапах выполнения проекта в целом можно с помощью, так называемой карты проекта, в которую преобразуется исходная сетевая модель. В этом случае каждая работа имеет информацию не только о ее длительности, но и о потребности в различных категориях работников. Карта проекта может быть получена после нахождения критического пути.
- число конструкторов
- механиков
- лаборантов.
Критический путь на карте проекта (календарном графике) изображается жирной прямой линией вдоль оси абсцисс в масштабе времени. Все остальные работы откладываются выше и ниже критического пути. Они изображаются тонкими линиями со стрелками, длина которых пропорциональна продолжительности работ. Пунктирными линиями показывают резервы работ по времени, (они играют вспомогательную роль, давая более наглядно представить взаимосвязь событий и резервов времени на работах).
Фиктивная работа вычерчивается только пунктирными линиями. При отсутствии резерва они изображаются на карте вертикальной пунктирной линией.
Под календарным графиком изображаются диаграммы потребности в работниках каждой категории.
Если решение задач 2 и 1 не дает нужных результатов (в плане выполнения директивных сроков), то вновь пытаются сократить критический путь за счет интенсификации труда на отдельных участках.
Следующим шагом на этом пути является параллельное выполнение работ (путем дробления работ большой длительности, если, конечно, это технологически возможно). При этом все работы с сетевой моделью начинаются заново.
Проводя оптимизацию СГ не возможно не затронуть фактор стоимости выполняемых работ. В практике решаемых задач, кроме оценки времени выполнения работ вводится так же и оценка их стоимости. При определении стоимости работ учитываются используемые ресурсы. Этот метод название “время - затраты”. Он заключается в установлении зависимости между продолжительностью и стоимостью работы с целью их оптимизации.
Один из вариантов постановки задачи может быть таким: при найденном критическом пути использовать ресурсы некритических работ и получить сеть с минимальными затратами на весь комплекс работ (задача 3). Предполагается, что увеличение сроков выполнения работ снижает их стоимость.
 Другой
вариант: за счет увеличения затрат на работы критического пути сократить
сроки выполнения работ этого пути, а значит и сроки выполнения всего
проекта (задача 1). Другой
вариант: за счет увеличения затрат на работы критического пути сократить
сроки выполнения работ этого пути, а значит и сроки выполнения всего
проекта (задача 1).
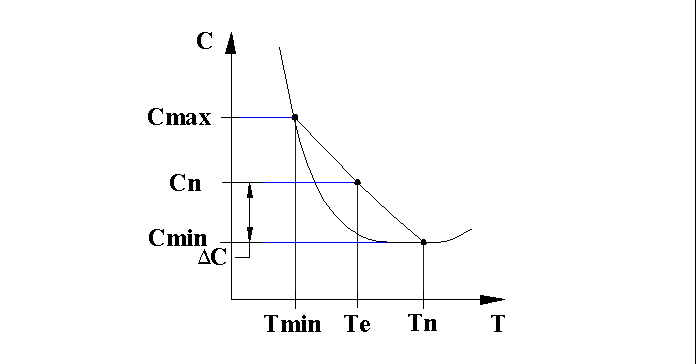
Для построения графиков “время - затраты” для каждой работы делаются
две пары оценок: а и б. Повышение затрат, при увеличении сроков
сверх нормально установленных, обеспечиваются не интенсивностью
выполнения работы, а оплатой исполнителей в течение времени, большего,
чем это необходимо. Из рисунка видно, что величину 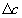 ,
необходимых для выполнения работ в сокращенное время, т. е. равно: ,
необходимых для выполнения работ в сокращенное время, т. е. равно: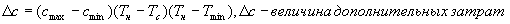
Для каждой работы должен быть рассчитан (на основе нормативов или схем) и построен свой график, характеризующийся наклоном апроксимирующейся прямой (а - б).
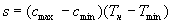 , где s- коэффициент возрастания
затрат, показывающий в какую сумму выливается сокращение работы
на 1 день.
, где s- коэффициент возрастания
затрат, показывающий в какую сумму выливается сокращение работы
на 1 день.
Тогда с учетом вышесказанного, самым очевидным вариантом решения задачи 3 (корректирование и оптимизация СГ) является подход основанный на использовании свободных ресурсов работ.
Рассмотрим его:
Пусть для комплекса работ (рис. Таблица.) длительности операций
выбраны так, что 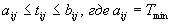 -минимально
возможное время выполнения работы; -минимально
возможное время выполнения работы;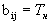 -нормальное
время продолжительности работы. -нормальное
время продолжительности работы.
Для конкретно выбранного варианта реализации работ известен критический путь и резервы времени для каждой работы конкретной зоны.
Стоимость выполнения проекта рассматривается, как сумма стоимости всех работ, составляющих сеть проекта:
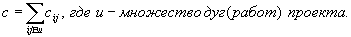
Если теперь рассмотреть новый план, полученный с учетом нормальных ограничений (там, где есть резервы), то очевидно, что с точки зрения затрат он будет наиболее экономичным.
Экономию на каждой работе подсчитать, взяв произведение коэффициента
(возрастание затрат 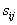 ,
пропорциональности линейной
апроксимации) ,
пропорциональности линейной
апроксимации) 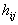 на приращение длительности работы
на приращение длительности работы 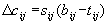 .
Полная экономия равна сумме этих произведений. Тогда стоимость нового
плана будет равна: .
Полная экономия равна сумме этих произведений. Тогда стоимость нового
плана будет равна: 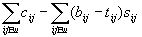 . .
Т.о. приведенный выше подход показывает, каким образом информация, полученная после расчетов параметров сети, может быть использована для улучшения плана путем удлиннения тем, где это возможно, некритических путей при Tкр= const.
Т. о. Из вышесказанного видно, что при оптимизации сетевых моделей во многих случаях существенную важность представляют задачи распределения ресурсов. При решении которых в расчет принимаются такие факторы, как:
- резерв времени; непрерывность работы; стоимость неиспользуемых ресурсов и др., причем в общем случае каждый из них снабжается весовым коэффициентом, отражающим его относительную важность. Выбор наилучшего варианта из нескольких производится на основе второго критерия.
Рассмотрим несколько вариантов формализации задач распределения ресурсов, допускающие постановку задач на оптимизацию (рис.1).
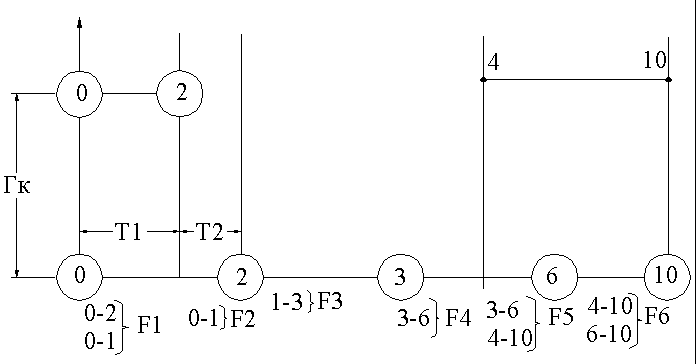
Рис. 1
ФОРМАЛИЗАЦИЯ. ЗАДАЧА МИНИМИЗАЦИИ ВРЕМЕНИ. (ЗАДАЧА 1)
Заключается в оптимальном распределении ресурсов по работам, т. е. в определении времени начала каждой работы, которое при заданных ограниченных ресурсах обеспечивало бы выполнение проекта в минимальное время.
Обозначим через А ресурс, доступный в каждый день выполнения проекта (например, численность рабочих).
Предположим, что каждая работа (ij) допускает перерывы при ее выполнении, и что для каждой работы (ij) задана ее длительность при известной интенсивности потребления ресурсов.
Обозначим через 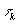 длину
k-го промежутка длину
k-го промежутка 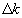 ,
другими словами, ширину ступеньки на графике загрузки (или на кате проекта
(см рис. 1)), причем: ,
другими словами, ширину ступеньки на графике загрузки (или на кате проекта
(см рис. 1)), причем: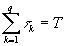 ,
где Т – время выполнения проекта. ,
где Т – время выполнения проекта.
Очевидно, под каждым промежутком 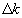 будут в линейной диаграмме расположены работы, которые сетевой график
позволяет выполнить одновременно, т.е. работы, принадлежащие одному
фронту. Суммарный ежедневный ресурс, необходимый для выполнения работ
фронта Fk, т. е. интенсивность
этого фронта определяется, как:
будут в линейной диаграмме расположены работы, которые сетевой график
позволяет выполнить одновременно, т.е. работы, принадлежащие одному
фронту. Суммарный ежедневный ресурс, необходимый для выполнения работ
фронта Fk, т. е. интенсивность
этого фронта определяется, как: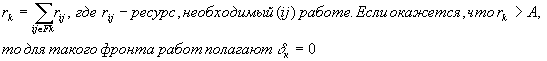 Т.о.,
считая неизвестными задачи продолжительности одновременного выполнения
определенных сочетаний работ, можно задачу оптимального распределения
истраченного ресурса, минимизирующего продолжительность Т выполнения
проекта, свести к следующей задаче линейного проектирования: найти Т.о.,
считая неизвестными задачи продолжительности одновременного выполнения
определенных сочетаний работ, можно задачу оптимального распределения
истраченного ресурса, минимизирующего продолжительность Т выполнения
проекта, свести к следующей задаче линейного проектирования: найти
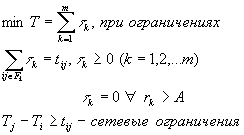
Решение настоящей задачи ручным способом можно выполнить с помощью двух методов: последовательного и параллельного. Идея методов заключается в распределении ресурсов по работам.
При первом способе ресурсы распределяются по работам последовательно (отдельно для каждой работы, от ее начала до конца).
Параллельный метод распределяет ресурсы ежедневно по всем работам, которые в этот день могут выполняться.
При распределении ресурсов пользуются, так называемыми пред-ния.
- направить ресурсы на выполнение работ с меньшим резервом.
- На работы, требующие наибольшего количества ресурсо-дней.
- На работы, требующие наибольшего количества людей.
- На работы с меньшим номером при равенстве всех человек.
Для параллельного метода после правила 1 ресурсы направляются на начавшиеся, но еще не завершенные работы (остальное все то же самое)
(задача 2)
Обратная задача – задача оптимального распределения ресурсов при заданном времени выполнения проекта.
Минимизировать стреднеквадратичное отклонение ежедневно потребляемого ресурса от его среднего потребления при заданном времени выполнения проекта Т.
Общая трудоемкость Атр работ может быть выражена формулой
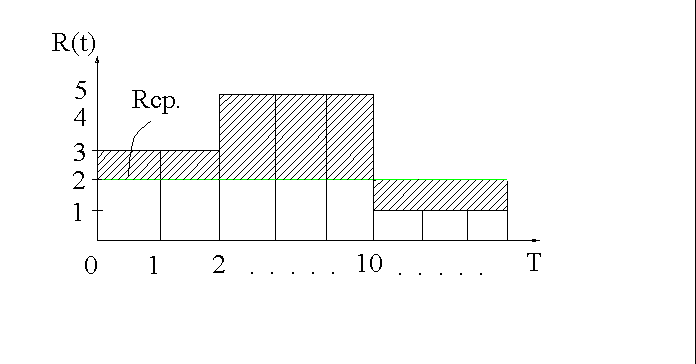
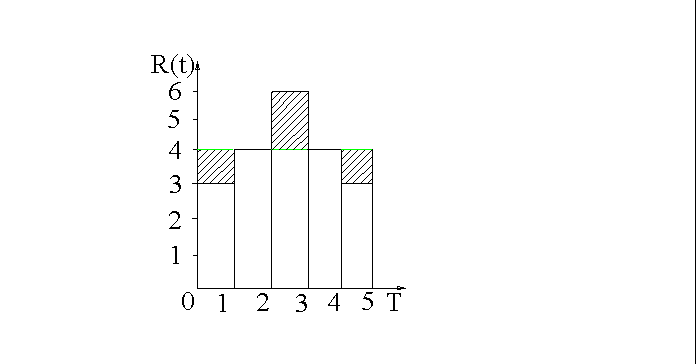
 ,
где R(t) – интенсивность потребляемого
ресурса в каждый момент времени t. ,
где R(t) – интенсивность потребляемого
ресурса в каждый момент времени t.
Среднее количество работников (средняя интенсивность потребления ресурса
в единицу времени) 
Мерой неравномерности ресурса можно считать интервал  , минимизация которого сводится к минимизации
, минимизация которого сводится к минимизации 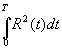
Т. е. задача сводится к минимизации суммы квадратов потребителей в ресурсах на каждый день. Эта сумма тем меньше, чем меньше изменение потребности в ресурсах при переходе от одного рабочего дня к другому.
Наименьшая сумма квадратов соответствует наиболее сглаженному решению.
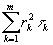
Принимая
прежние обозначения Fk; 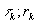 ,
получим ,
получим 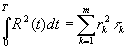 ,
что позволяет при прежних допущениях свести поставленную к следующей задаче
математического программирования: ,
что позволяет при прежних допущениях свести поставленную к следующей задаче
математического программирования:
Минимизировать
При ограничениях: 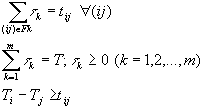
Следует отметить, что изложенные выше подходы справедливы, когда взаимозаменяемость работников достаточно велика.
Рассмотренный выше подход действительно позволяет выбрать наиболее сглаженное распределение ресурсов, которое в идеале является равномерным, как показано на рис. Однако, иногда на практике требуется выбрать решение с параболическим, а не прямоугольным распределением. (параболический профиль предпочтителен, когда перед началом работ требуется подготовка персонала).
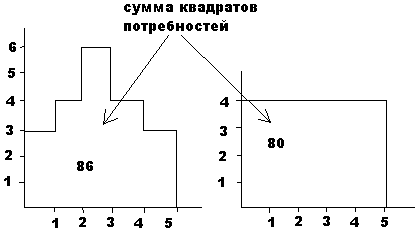
В этом случае в качестве критерия следует взять дисперсии ежедневных
изменений требуемых ресурсов. Соответствующий критерий будет иметь вид:  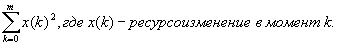 для вышеприведенного рисунка этот критерий равен: для случая а -
для вышеприведенного рисунка этот критерий равен: для случая а - 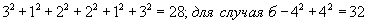
Дисперсия является мерой колебаний (флуктуаций), поэтому дисперсия ресурсных изменений характеризует сглаженность ресурсного профиля и используется, как целевая функция при нахождении оптимального ресурсного профиля. Сформулируем модель:
Пусть Т- длительность проекта; W – количество ресурсо-дней; x(k) – ресурсное изменение в момент k; r(k) – потребность в ресурсе в момент k.
Количество ресурсо- дней может быть представлено следующим образом:
 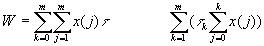 (1)
(1)
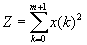
Ресурсы
должны быть целиком использованы до конца проекта; следовательно 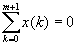 (2)
(2)
Целевой функцией является дисперсия ресурсных изменений
 Т.
к . в (3) m=const и Т.
к . в (3) m=const и  =0,
то целевая функция Z примет вид =0,
то целевая функция Z примет вид 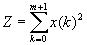
После минимизации (аппроксимации) этой функции по методу множителей Лагранжа
оптимальная функция потребности в ресурсах для каждого интервала
k (k=1...m) приобретет вид :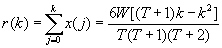
ЗАДАЧА №3
Одним из классов ресурсных задач для решения, которых существуют точные методы, являются задачи, учитывающие прямые затраты на производство работ (задача 3).
Математическая модель такой задачи имеет следующий вид:
Пусть для каждой работы ( ij) комплекса U задана функция “время - стоимость”:
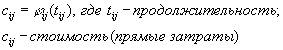
Допускаемые технологические пределы продолжительности каждой работы заданы
следующим образом: 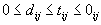 (1)
(1)
Кроме того, задан директивный срок Тдир. Завершения комплекса, т. е. условия Ткр <=Тдир. (2)
Требуется определить такие продолжительности tij работ (ij), чтобы выполнялись условия (1) и (2) и суммарные затраты:
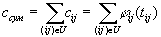 были минимальными. (где U – множество
других работ проекта). При решении задачи должны быть учтены так же сетевые
ограничения:
были минимальными. (где U – множество
других работ проекта). При решении задачи должны быть учтены так же сетевые
ограничения: 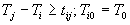
|
|







