Химико-технологический процесс как система

Одно из важнейших понятий современной науки—система, Возникнув в кибернетике, оно приобрело статус философской ка­тегории—настолько широко и обще его применение .

Система—это совокупность элементов, отличающаяся двумя особенностями. Во-первых, сущность системы невозможно понять, рассматривая только свойства отдельных элементов. Для системы. существенен способ взаимодействия элементов, выражен­ный в ее структуре. Во-вторых, система функционирует обя­зательно во взаимодействии с окружающим миром. Без понимания этого взаимодействия также невозможно понять ее сущность. По сути, любой объект природы и общества является системой. И в научном анализе чрезвычайно важно это учитывать. Важен системный подход .

 

Пример 1 . Превращение несистемы в систему .

Оборудование, предназначенное для монтажа технологической установки, ле­жит на складе. В этом виде его нельзя рассматривать как систему: элементы (единицы оборудования) не взаимодействуют друг с другом. При монтаже обо­рудования и сборке технологической схемы возникает структура, взаимодействие элементов. Но чтобы установка стала системой, необходимо еще взаимодействие-с окружающим миром: воздействие внешнего мира на систему (например, пода­ча сырья и энергии) и воздействие системы на внешний мир (выпуск продук­ции). Без этого структура окажется бессмысленной, а системность установки будет лишь кажущейся. Конечно, если установку временно законсервируют, она не перестанет быть системой, но лишь постольку, поскольку предполагается воз­можность вышеназванного взаимодействия.

 

Системы, которыми мы будем заниматься в этой книге,—хими­ко-технологические процессы. Элементами химико-технологическо­го процесса являются проходящие в нем процессы: химические реакции, тепло- и массообмен, движение фаз и другие. Системный подход к химической технологии связан с пониманием того, что анализ этих процессов, производимый порознь, не дает еще воз­можности судить обо всем процессе в целом. Поэтому при анали­зе химико-технологического процесса особое внимание следует обращать на взаимодействие составляющих его элементов.

Внешние связи системы можно представить схемой, изображен­ной на рис. 1. Прямоугольник на рисунке символизирует систе­му. Буквами h, x, z обозначены воздействия, оказываемые на систему. Будем называть их входами системы, или факто­ра ми. В некоторых случаях для краткости факторы h₁, h₂, ...,h_m в их совокупности будем обозначать через Н (вектор факто­ров А), факторы x₁,...,x_п—через X, факторы z₁, z₂,...—соответ­ственно через Z. Обозначения y₁,...,y_k относятся к воздействиям си­стемы на окружающий мир, это—результаты функционирования системы; будем называть их выходами системы, или откликами (имеется в виду отклик системы на воздействие факторов). К их числу относятся количество про­изведенного продукта, его качественные показатели, себестоимость, прибыль предприятия, количество выбрасываемых в окружающую среду вредных примесей и множество других пока­зателей .

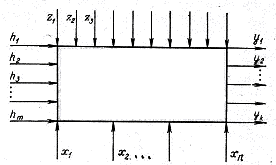
Рис. 1. Схема внешних связей системы

 

 

Входы на рис. 1 разделены на три группы: H, X, Z. Факторы Н и Х— контролируемые входы. Это те воздействия, кото­рые мы контролируем (измеряем) в процессе функционирования системы .

При этом h₁, h₂, ...,h_m—факторы, контролируемые, но нерегулируемые. Мы измеряем их, знаем их величины, но не изменяем их произвольно. Нерегулируемость части входов мо­жет быть связана с разными причинами. Прежде всего, некоторые факторы трудно регулировать: трудно изменять диаметр работаю­щего аппарата (а диаметр—фактор, который может существенно влиять на ход процесса); трудно регулировать состав сырья (что завод получил, то и надо перерабатывать) и т. д. Иногда органи­зовать регулирование технически нетрудно, но регулирование •слишком большого числа факторов настолько усложняет систему управления процессом, что предпочитают оставлять нерегулируе­мыми те из факторов, которые влияют слабее прочих .

Х — вектор контролируемых и регулируемых вхо­дов. Это те воздействия, которые мы изменяем, чтобы управлять системой. Поэтому обычно их называют управляющими фак-т о р а м и, или коротко управлениями. Наконец, Z—вектор неконтролируемых факторов. Это те воздействия на систему, которые находятся вне нашего контроля .

Возможны три основных причины того, что тот или иной фак­тор оказывается неконтролируемым. Во-первых, объект может быть плохо изучен, вследствие чего мы не знаем, что данный фак­тор существенно влияет на поведение объекта, и поэтому не конт­ролируем этот фактор .

 

Пример 2 . Неконтролируемый фактор .

До того, как Ч. Гудьир установил, что взаимодействие с серой приводит к вулканизации резины, этот фактор был неконтролируемым. В многочисленных попытках получить из каучука более ценный продукт Гудьир обрабатывал его и серосодержащими веществами (например, парами серной кислоты), причем в ряде случаев получал обнадеживающие результаты; но пока он не понял, что действующий фактор—именно сера, вулканизация не была изобретена.

 

Вторая причина неконтролируемости фактора—неумение его контролировать. Есть один важный фактор, сильно влияющий на самые разнообразные системы, контролировать который мы умеем очень плохо. Это индивидуальность и душевное состояние челове­ка, работающего с данной системой. Мы далеко не всегда знаем,. какие именно параметры этого сложного фактора оказывают влия­ние и как их измерять .

Сейчас проблеме взаимодействия человека с теми системами, которыми он управляет, уделяется очень большое внимание. Иног­да получаемые результаты оказываются неожиданными .

 

Пример 3 . Особенности поведения лучших рабочих .

В производственных условиях изучены особенности трудовых приемов, влияющих на качество продукции при изготовлении резисторов. По результатам работы удалось выделить две группы рабочих: «средние» и «хорошие».

Исследование показало, что в ходе технологического процесса «средние» ра­бочие стараются поддерживать параметры процесса как можно ближе к регла­ментным значениям.

«Хорошие» рабочие все время «покачивают» параметры, слегка (в допусти­мых пределах) отклоняют их значения от регламентных, стремясь найти усло­вия, которые в данный момент оптимальны. Найдя оптимум и поработав в этих условиях некоторое время, такой рабочий снова начинает «покачивать» пара­метры, выясняя, в какую сторону сместился оптимальный режим. Интересно, что сами рабочие не могли сформулировать, какие особенности их работы обеспе­чивают успех.

 

Наиболее распространена третья причина, по которой мы не контролируем множество входных воздействий. Каждое воздейст­вие из этого множества слишком слабо, чтобы стоило его контро­лировать. С другой стороны, таких слабых воздействий столь много (практически бесконечно много), что все их контро­лировать невозможно. На химико-технологический процесс как-то влияют и микропримеси, попадающие из воздуха и из аппаратуры, и солнечный луч, пробившийся в окно и слегка подогревший аппа­рат, и вибрации от проехавшего за стеной грузовика, чуть-чуть уплотнившие слой катализатора... стоит ли продолжать ?

При этом каждый из этих факторов влияет очень слабо, но их столь много, что совокупное их влияние оказывается весьма ощу­тимым. Важно отметить, что это влияние носит случайный характер: не контролируя входы Z, невозможно предсказать» как они повлияют в той или иной момент. В эксперименте их влия­ние появляется в случайных ошибках опытов; на про­изводстве—в случайных возмущениях режима. В це­лом влияние неконтролируемых воздействий часто обозначают тер­мином шум. Учет шума необходим в большинстве технологиче­ских задач .

Источник шума может заключаться и внутри системы, но это не изменит наших рассуждений .

Математические описания функционирования системы в общем виде представляют собой систему уравнений вида :

уi=Фi (Н, X, Z)                                                                                        (1)

В принципе каждое из уравнений (1) определяет зависимость. 1-го выхода от всех входных воздействий. Но установить вид функ­ции Ф принципиально невозможно: мы не знаем даже списка аргу­ментов этой функции — ведь факторы Z нам неизвестны. К счастью ,.

во многих случаях каждое из уравнений (1) достаточно точно можно представить в виде

y_i = F_i (H, X) + R_i (Z)                                                                                         (2)

Здесь функция разбита на два слагаемых: зависимость Fi от конт­ролируемых факторов и шум R_i,-. Теперь уже задача создания ма­тематической модели процесса приобретает смысл: нужно уста­новить вид функции F и оценить шум R. Часто под мате­матической моделью понимают именно совокупность функций Fi(H, X), выделяя оценку шума в отдельную задачу. Мы тоже будем называть математической моделью (математическим описа­нием) систему уравнений

y_i = F_i (H, X)                                                                                                     (3)

помня, однако, что в таком виде модель по существу неполна; в. любом ответственном случае оценка шума обязательна.

 Два подхода к описанию системы.

Вид функций (3) можно получить из двух разных подходов.

Первый можно назвать структурным. Суть его заключает­ся в следующем. Для создания математической модели системы мы прежде всего исследуем ее структуру—составляющие систему элементы и характер их взаимодействия. Применительно к техно­логическому процессу это означает расшифровку его механизма.. В результате получается схема процесса—его мысленная модель.. Для химико-технологического процесса мысленная модель на фи­зическом языке содержит прежде всего представления о механиз­ме реакции, характере движения потоков, процессах переноса теп­ла и вещества и о взаимном влиянии химизма, гидравлики, тепло и массопереноса.

Записав эту схему на языке математики, получаем некую си­стему уравнений, описывающих процесс. Обычно на этом этапе уравнения получаются в общем виде—в них входят некоторые пока неизвестные коэффициенты (константы скоростей реакций, коэффициенты тепло и массоотдачи и др.). Эти коэффициенты на­зывают параметрами модели. Для определения парамет­ров ставится эксперимент (на моделях, а иногда и на оригинале, если таковой имеется), результаты которого позволяют получить модель в полном виде, со всеми коэффициентами.

Второй подход к описанию системы—эмпирический. Дру­гое его распространенное название — метод черного ящика. Предположим, что структура интересующей нас системы скры­та от нас (как бы заключена в «черный ящик»). Значит ли это, что о системе ничего невозможно узнать и, главное, что нельзя ею управлять? Нет, не значит. Как бы черен ни был ящик, у системы есть важные контакты, которыми можно воспользоваться для ее анализа и управления ею. Эти контакты—входы и выходы си­стемы.

Давайте изменять значения входов и определять, как будет при этом изменяться отклик. Каждый такой акт—изменение входов и определение отклика — есть не что иное, как эксперимент. Про­ведя определенное число экспериментов, мы можем их результаты описать эмпирическим уравнением или системой эмпирических уравнений. Эти уравнения и будут математической моделью, кото­рой можно воспользоваться для моделирования данной системы и управления ею.

Долгое время в науке господствовало убеждение, что истинно научным яв­ляется лишь структурный подход, а подход эмпирический—это нечто неполно­ценное, второстепенное, вспомогательное, нечто такое, что пригодно в практиче­ских задачах, а также на начальном этапе научного исследования; истинная же наука начинается с установления механизма, с расшифровки структуры. Одним из плодотворных положений кибернетики является утверждение того, что во мно­гих задачах метод черного ящика может оказаться основным способом исследо­вания, что это полноправный научный метод и что в каждом конкретном случае надо оценить преимущества и недостатки обоих подходов.

Необходимо подчеркнуть следующее важнейшее обстоятельст­во. Будучи противоположностями, оба подхода образуют тесное единство. При этом в любом реальном случае наличествуют эле­менты и того, и другого подхода. Ни абсолютно структурное, ни абсолютно эмпирическое описание невозможны,

В любом сколько-нибудь серьезном случае все описание объек­та, как бы хорошо он ни был изучен, нельзя построить на чисто теоретической основе. Какие-то параметры всегда придется опре­делять из опытов, и опытным же путем проверять адекват­ность модели—достаточную точность ее соответствия ориги­налу.

С другой стороны, каким бы черным ни был наш ящик, мы обязательно имеем какие-то представления о его структуре. Без этого вряд ли удастся выделить контролируемые входы и понять, каких откликов можно ожидать от системы.

Любое эмпирическое описание отражает, хотя и в неявной форме, механизм процесса. Иногда это отражение оказывается на­столько характерным и точным, что анализ эмпирического уравне­ния прямо приводит к раскрытию механизма. Вспомним, что урав­нения Кеплера или Бальмера были чисто эмпирическими, пока работы Ньютона и Бора их не объяснили. Эмпирическое уравнение обязательно содержит в себе структуру, только структуру не­расшифрованную. Поэтому четкое противопоставление обоих под­ходов носит характер методический, а не прикладной. В практических задачах наблюдаются самые разнообразные соотношения между уровнями структурности и эмпиричности применяемых ме­тодов.

Гидродинамическую задачу можно исследовать, решая для частного случая уравнение Навье — Стокса — это будет наиболее структурный вариант, но в здесь, скорее всего, придется вносить эмпирические поправки.

Уравнения Навье—Стокса можно использовать только для вывода крите­риев подобия, а дальше перейти к экспериментальному изучению процесса.

Можно совсем не прибегать к этому уравнений, а выводить критерии подо­бия на основе метода размерностей—структурность подхода будет еще слабее.

Наконец, при обработке опытных данных можно отказаться и от критериальной формы, еще усилив тем самым эмпиричность подхода.

Тем не менее, чаще всего подход к решению той или иной кон­кретной задачи можно охарактеризовать как в основном структур­ный или эмпирический. Поэтому целесообразно оценить сильные и слабые стороны обоих подходов.

Главное достоинство эмпирического подхода — простота.. Особенно существенно оно сказывается при изучении очень слож­ных процессов.

Главная его слабость — малая надежность экстрапо­ляции. В пределах изменения переменных, изученных в опытах, предсказание поведения процесса (интерполяция) обычно может проводиться достаточно точно. Но закон изменения функ­ций отклика за изученными пределами нам неизвестен, и можно допустить серьезную ошибку, полагая, что процесс по-прежнему обязательно будет подчиняться выведенным нами эмпирическим уравнениям.

 

Пример 4. Попытка экстраполяции эмпирической зависимости.

Некоторое свойство вещества зависит от температуры. Не зная механизма зависимости, мы провели опыты и получили следующие данные:

 

По этим данным нетрудно рассчитать зависимость у от Т. В изученных пре­делах ее можно выразить уравнением:

у = 1,000—9,62. 10^-5 (T—278) —3,75- 10^-6 (T —278)²                                                                       (4)

Рассчитаем по уравнению (4) значения у при Т=350; 370; 380 К. Полу­чим соответственно y=0,974; 0,959, 0,942.

В действительности, значения у при этих температурах составляют: 0,974;

0,960; 0,00056. Для двух первых точек получено вполне удовлетворительное со­гласование, для третьей—разительное несходство. Если бы мы заранее знали, что y—плотность воды при атмосферном давлении, т. е. достаточно хорошо представляли структуру объекта, то никаких неожиданностей не было бы.

 

 Разумеется, ситуация упрощена: в столь ясных случаях эмпи­рический подход вряд ли стоит применять. Именно температурные зависимости очень часто плохо поддаются экстраполяции. В практике моделирования одним из важнейших случаев экст­раполяций является масштабирование: предсказание того, как изменятся параметры процесса при переходе от малой модели к большому оригиналу. На основе эмпирических зависимостей эта задача, как правило, решается гораздо хуже, чем при структур­ном подходе.

Главное достоинство данных, полученных на основе структур­ного подхода — это их большая прогностическая мощ­ность. Зная достаточно полно механизм какого-либо процесса, мы можем с большой степенью достоверности предсказывать его поведение в самых разнообразных условиях. Поэтому, как гласит известный афоризм, «нет ничего практичнее хорошей теории».

Слабое место подхода—трудность создания хорошей теории сложных процессов. Если выделить лишь один элемент химико-технологического процесса — его гидродинамику, то приходится считаться с отсутствием на сегодня сколько-нибудь удовлетвори­тельной теории турбулентности. Далее, современная химия знает 'сотни тысяч веществ и, если бы мы задались целью всерьез рас­шифровать механизмы реакций получения всех этих веществ, то вряд ли достигли бы этой цели в обозримый срок. Подобные за­труднения встречаются на каждом шагу. Понятно, что рассчитать эмпирические уравнения, как правило, бывает проще, чем полу­чить информацию, достаточную для расшифровки механизма процесса. Можно выделить области, где подход в основном приобретает черты той или иной противоположности. Во-первых, эмпирические модели лежат в фундаменте науки: исходные ее данные, ее аксиомы—суть эмпирические модели. Далее, метод «черного ящи­ка» часто оказывается целесообразным применительно к очень сложным системам, на пути расшифровки структуры которых мо­гут возникнуть непреодолимые трудности. Наконец, эмпирический подход имеет смысл применять при исследовании систем, не пред­ставляющих для нас большой важности, на исследование струк­туры которых не стоит затрачивать много сил. Лучше быстро описать такой объект эмпирической зависимостью и использовать ее для управления. Объекты, представляющие для нас значительный интерес, дли­тельный во времени, структура которых не слишком сложна, целе­сообразно исследовать на базе структурного подхода. Так, для важнейших процессов химической технологии, таких как синтез .аммиака или каучуков, нужно как можно подробнее исследовать механизм, создать математические модели, отражающие все детали структуры. Результаты окупят затраты. Тот же подход оптима­лен для сравнительно простых процессов. В то же время некоторые «малые» органические синтезы, например синтезы ряда ле­карств, не стоит и пытаться полностью описать с этих позиций: процесс столь сложен, что пока мы расшифруем его кинетику, лекарство морально устареет и будет заменено. Здесь лучше быст­ро научиться управлять процессом, считая его черным ящиком.

Если процесс и важен, и сложен, иногда бывает полезно раз­бить его изучение на этапы: на первом—изучать его эмпириче­ски, что облегчает быстрое освоение; на втором—проводить уг­лубленное изучение механизма, которое позволит улучшить резуль­таты, полученные ранее.

 

Структура математического описания при структурном подходе.
Процессы, применяемые в химической технологии, крайне разнооб­разны по механизмам. Поэтому дать общую схему математическо­го описания процесса весьма затруднительно. Однако некоторые весьма общие черты описания можно отметить.

Важнейшие законы, на которых базируются математические модели, — это законы сохранения, выражением которых являются уравнения баланса. Баланс может быть состав­лен для определенной технологической операции, но в непрерыв­ных процессах удобнее составлять уравнения баланса за едини­цу времени.

В основе описаний протекания химических реакций, массообмена и теплообмена лежат обобщенные уравнения материального баланса и обобщенные уравнения теплового баланса (шире—ба­ланса энергии, но во многих важных задачах он сводится к балан­су тепла).

Обобщенное уравнение материального баланса имеет вид:

Приход вещества—Расход вещества = Накопление вещества                      (5)

Разность между приходом и расходом вещества равна измене­нию количества вещества в рассматриваемом объеме. Если приход больше расхода, то вещество накапливается (положительное на­копление), если меньше, то убывает (убыль, или «отрицательное накопление»). В стационарном режиме не может происходить ни убыль, ни накопление; в этом случае обобщенное уравнение (5) переходит в обычное уравнение материального ба­ланса:

Приход вещества = Расход вещества                                                                   (6)

Уравнения (5) и (6) можно применять как к каждому веще­ству в отдельности, так и ко всей совокупности веществ, участвую­щих в процессе.

Соответствующим образом для тепловой энергии , получаются обобщенное уравнение теплового баланса:

Приход тепла — Расход тепла = Накопление тепла                                         (7)

и, в стационарном режиме, обычное уравнение теплово­го баланса:

Приход тепла = Расход тепла                                                                                (8)

Необходимо помнить, что строго говоря, закона сохранения ко­личества тепла не существует. Термин «накопление тепла», стоя­щий в правой части уравнения (7), не точен; на самом деле уве­личивается (или уменьшается) количество не тепла, а внутренней энергии, энтальпии или иной функции состояния, в зависимости от процесса. В уравнениях (7) и (8) следовало бы учесть работу. Но во многих процессах основные энергетические эффекты—теп­ловые, так что можно пользоваться этими уравнениями, разумеет­ся, учитывая их нестрогость.

Сложность структуры химико-технологического процесса, в частности, проявляется в том, что составляющие его элементарные процессы протекают на разных уровнях: от наинизшего (уровень молекулы) до высшего (уровень цеха или завода). Эта разноуровневость должна найти отражение в описании. Один из наиболее разработанных способов такого отражения иерархическая структура математической модели, предложенная М. Г. Слинько. Модель строится путем последовательного пе­рехода в описании процесса с одного уровня на другой.

1. Молекулярный уровень. Описание процессов, протекающих в масштабе порядка расстояния между молекулами. Их закономер­ности—это прежде всего закономерности химической кине­тики.

2. Уровень малого объема. На этом уровне объектом описания является, например, процесс на одном зерне катализатора, или в пузырьке газа, поднимающемся в барботажном слое, и в обтекаю­щей его жидкости, или на одном элементе насадки в насадочной колонне, и т. д. Здесь закономерности предыдущего уровня уже недостаточны; необходимо дополнить их закономерностями суще­ственных в этом масштабе процессов тепло- и массопереноса. Ана­лиз кинетических закономерностей в условиях одновременного про­текания процессов переноса—предмет научного направления, на­зываемого макрокинетикой.

3. Уровень рабочей зоны аппарата (слой катализатора, барботажный слой, насадочный слой и т. п.). На этом уровне необходи­мо учитывать эффекты, связанные с характером, движения по­тока. В ряде случаев (например, при гомогенных реакциях) на этот уровень можно перейти прямо с первого.

4. Уровень аппарата. При переходе на него учитывают число, конфигурацию, взаимную связь и взаимное расположение рабочих зон. Например, аппарат может содержать несколько слоев катали­затора, между которыми располагаются промежуточные теплооб­менники.

5. Уровень агрегата. Здесь учитываются взаимные связи между аппаратами.

 

Модель каждого высшего уровня содержит модели низших уровней и соотношения, описывающие переход с одного уровня на другой. Такой подход часто позволяет анализировать и моделиро­вать процесс по частям, что существенно упрощает анализ; в то же время при этом не упускается из виду структура—характер свя­зей уровней. В дальнейшем изложении рассматриваются законо­мерности трех первых уровней, хотя и в несколько иной последо­вательности, чем приведенная здесь.

 

Эмпирические модели. 
Проводя опыты при эмпирическом под­ходе мы не знаем, в каком виде следует получать функцию откли­ка. Если у зависит только от одного х, а вид зависимости доста­точно прост, то можно судить об этом виде на глаз, по графику. Если аргументов несколько или если график сложен, то этот путь закрыт. Поэтому для нахождения вида функции (3) обычно пользуются тем, что большинство функций, с которыми приходится иметь дело на практике, можно разложить в ряд Тейлора (степен­ной ряд). Если ограничиться несколькими первыми членами ряда, получится представление функции многочленом (полиномом). Этот многочлен есть приближенное выражение неизвестной функ­ции F(H,X); качество приближения определяется величиной остатка ряда—той его части, которую мы отбрасываем. Что­бы наше приближение удовлетворительно описывало процесс, нужно, чтобы остаток был невелик по сравнению с шумом. Тогда дальнейшее уточнение функции теряет смысл: мы не можем выя­вить, действительно ли следующие члены отражают уточненную функцию или они связаны лишь со случайными ошибками опыта.

Обычно вначале рассчитывают более простые многочлены; от­клонение опытных точек от расчетных значений сравнивают со слу­чайной ошибкой эксперимента. Если обе величины — одного поряд­ка, то описание считают удовлетворительным. Если отклонение нельзя объяснить случайной ошибкой, то рассчитывают более сложный многочлен.

Так, рассмотрим случай, когда у зависит от трех переменных x1, x2 и x3. Первое возможное предположение: у на самом деле не зависит от контролируемых входов, и все его отклонения от сред­него значения у объясняются случайными ошибками

Y = b₀ =`yи                                                                                                             (9)

Здесь и далее b—эмпирический коэффициент.

Если проверка покажет, что отклонения у от значения у дей­ствительно имеют тот же порядок, что и случайная ошибка опы­тов, то в дальнейшем можно пользоваться формулой (9), т. е. считать у константой. Если различия между опытными и расчетны­ми значениями у нельзя объяснить случайными ошибками, то уравнение (9) неадекватно и нужно проверить следующее приближение — линейное:

y = b₀ + b₁x₁ + b₂x₂ + b₃x₃                                                                                                                                    (10)

Проверка производится снова. Если неадекватно и выражение (10), то обрабатывают результаты в виде многочлена второго порядка:                                                

у = b₀ + b₁x₁ + b₂x₂ + b₃x₃ + b₁₁x1² + b₂₂x₂² + b₃₃x₃² + b₁₂x₁x₂ + b₁₃x₁x₃ + b₂₃x₂x₃ (11)

При неадекватности этого уравнения можно проверить много­член 3-го порядка, и т. д.

По мере роста порядка многочлена точность описания растет, но одновременно все усложняется трактовка модели — ана­лиз влияния каждого входа. Кроме того, чем больше коэффициен­тов содержит уравнение, тем больше опытов необходимо провести для их нахождения: минимальное число опытов равно числу коэф­фициентов, а для возможности оценки адекватности нужно прове­сти больше опытов, чем будет коэффициентов. Значит, для полу­чения линейной модели (10) опытов должно быть не менее 4, для модели (11)—не менее 10, а для модели 3-го порядка с тремя аргументами—уже как минимум 20. Уравнения порядка выше третьего (при более чем одном аргументе) на практике встреча­ются редко.

Представление эмпирических зависимостей многочленами встречается наиболее часто. Это связано с тем, что математические свойства таких приближенных формул хорошо изучены и с ними удобно обращаться. Правда, некритическое использование поли­номиальных формул (формул в виде многочленов) не всегда при­водит к успеху. Некоторые свойства объекта часто удобнее отра­жать при помощи формул, содержащих функции иных классов.

Так, при описании колебательных процессов, несомненно, удоб­нее использовать тригонометрические функции. Если пределы из­менения невелики, такой процесс можно описать и многочленом, но он будет неоправданно сложным.

Другой случай легко понять из примера.

 

Пример 5. Описание процесса в пограничном слое.

Необходимо подобрать форму эмпирического уравнение для закона затуха­ния турбулентных пульсаций скорости вблизи твердой стенки. Интенсивность пульсации обозначим через х, а расстояние от стенки — через I. Известно крае­вое условие: y=0 при b=0/ Функцию y(I) можно было бы искать в виде

H = b₀ + b₁ + b₁₁l₂² +...

Но тогда соблюсти краевое условие можно лишь, положив b₀=0. Получается довольно специальная категория полиномов без свободного члена. Описание ха­рактера затухания такой формулой может потребовать довольно многих пара­метров.

Есть, однако, более простая зависимость

H= Al^m                                                                                                                                                                                    (12)

При такой форме записи краевое условие удовлетворяется при любом значении m>0, а модель содержит лишь два параметра (A и m).

 

Степенная форма, аналогичная уравнению (12), удобна, на­пример, для записи зависимости критерия Нуссельта от критериев Рейнольдса и Прандтля, поскольку практически Nu®0 при Re®0 или при Рr®Q

Nu = A Re^m Prⁿ                                                                                                             (13)

Встречаются и иные удобные формы записи, но наиболее распро­странены многочлены.