Лабораторная
работа №3
Оптимизация
ресурсного профиля
Теоретические
основы
После расчета сетевой модели,
в качестве выходных данных, мы получаем перечень работ с временами их
начала и, как следствие, ежедневную занятость ремонтного персонала. Далее
решаются подзадачи оптимального распределения ресурсов при заданном времени
выполнения проекта.
Рассмотрим постановки задач
оптимизации сетевой модели остановочного ремонта путем перемещения некритических
работ. Рассмотрим несколько критериев.
1. Критерий – дисперсия ресурсных изменений.
Проводя оптимизацию с помощью этого критерия,
выбирается решение соответствующее практической потребности, т.е. профиль
ресурсов с параболическим распределением без значительного увеличения
или уменьшения количества рабочего персонала. Криволинейный профиль может
быть предпочтительным, если, например, требуется подготовка персонала.
Для того, чтобы получить параболический профиль ресурсов, необходимо минимизировать
флуктуации ежедневных изменений используемых ресурсов. В качестве показателя
флуктуации используется дисперсия. Для минимизации дисперсии ежедневных
изменений необходимо минимизировать суму квадратов этих изменений.
В приведенной ниже модели используется фиксированная
длительность ремонта (продолжительность критического пути сетевой модели
ремонта).
Введем обозначения:
N
– длительность остановочного ремонта;
W – количество
ресурсо-дней;
r(k)
– потребность в трудовом ресурсе в
момент времени k;
x(k) –
ресурсное изменение в момент времени k;
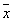 – среднее ресурсное изменение за всю
длительность остановочного ремонта.
– среднее ресурсное изменение за всю
длительность остановочного ремонта.
 (1)
(1)
Т.к. ресурсы должны использоваться
целиком до конца проекта, то
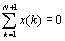 (2)
(2)
Целевой функцией является
дисперсия ресурсных изменений:
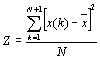 (3) (3)
Из уравнений (1-2) находим
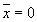 .
Если предполагается проводить оптимизацию путем перемещения работ в
пределах частных запасов времени, то в выражении (3) N=const
и .
Если предполагается проводить оптимизацию путем перемещения работ в
пределах частных запасов времени, то в выражении (3) N=const
и 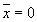 ,
поэтому целевая функция принимает вид: ,
поэтому целевая функция принимает вид:
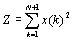 (4)
(4)
Следовательно: необходимо
найти такой вариант начала работ, чтобы
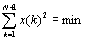
при ограничениях: 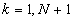 ; ;
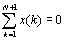 ; W=const. ; W=const.
2. Критерий – сумма квадратов потребностей
в ресурсах.
Сравнение сумм квадратов
потребностей в ресурсах для каждой единицы времени позволяет выбрать наиболее
сглаженное распределение, которое в идеале является равномерным. Эта сумма
тем меньше, чем меньше изменение потребности в ресурсах при переходе от
одного рабочего дня к другому. Наименьшая сумма квадратов соответствует
наиболее сглаженному решению.
Введем обозначения:
N
– длительность остановочного ремонта;
W – количество
ресурсо-дней;
r(k)
– потребность в трудовом ресурсе в момент
времени k.
Целевая функция в данном
случае будет выглядеть следующим образом:
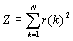 , ,
при ограничениях: 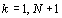 ;
W=const. ;
W=const.
|





