



Методика автоматизированного моделирования процессов самоочищения реки с малым расходом воды в условиях неопределенности.
В отечественной и зарубежной литературе описано большое число математических
моделей распространения примесей в водных потоках, учитывающих процессы
аэробного окисления органических соединений, нитрификации, денитрификации,
роста и отмирания планктона и т.п. [1-5] Все эти модели предназначены для
исследования конкретных объектов. Применение их для других аналогичных
объектов связано с серьезными трудностями, поскольку использование традиционных
методов идентификации предполагает проведение большого числа экспериментов.
К тому же большинство известных моделей относится к классу детерминированных
, тогда как природные водоемы – термодинамически открытые системы, подверженные
влиянию многочисленных неконтролируемых внешних воздействий, и процессы,
протекающие в них , имеют вероятностный характер. Кроме того, векторы входных
воздействий и выходных реакций имеют исключительно большую размерность.
В итоге это осложняет использование известных моделей в конкретной ситуации.
Между тем для рассматриваемых объектов часто имеется разнообразная,
хотя и не систематическая информация о качественном состоянии их водной
среды, полученная региональными, городскими или заводскими гидрохимическими
лабораториями в течение ряда лет. Однако отдельные показатели качества
были определены для различных сечений объекта; некоторые из них недостаточно
точны из-за несовершенства техники измерений. Использование такой информации
при моделировании стало возможно только с развитием теории нечетких множеств.
[6].
Данная работа [7] посвящена разработке методики моделирования водных
потоков, позволяющей построить адекватную математическую модель при наличии
качественной и неполной количественной информации о поведении объекта.
Описание методики. Представим модель, выбранную в качестве возможного варианта для описания био-физико-химических
процессов, характерных для исследуемого объекта, в виде:
![]() (1)
(1)
где ![]() - некоторый функциональный оператор, отображающий пространства всех начальных
состояний объекта
- некоторый функциональный оператор, отображающий пространства всех начальных
состояний объекта ![]() , параметров
, параметров ![]() и независимых входных переменных
и независимых входных переменных ![]() ,
реализованных на интервале времени
,
реализованных на интервале времени ![]() в пространство выходных переменных
в пространство выходных переменных ![]() .
.
Имеющуюся количественную и качественную информацию о поведении объекта представим следующим образом:
1. Детерминированные ограничения на выходные переменные модели
![]() (2)
(2)
В результате ограничений (2) в пространстве
реакций можно выделить гиперпараллелепипед ![]() ,
объем которого
,
объем которого
![]()
2. Функциональные ограничения
![]() ,
(3)
,
(3)
где ![]() - некоторые функции от
- некоторые функции от ![]() ,
заданные в явном или неявном виде.
,
заданные в явном или неявном виде.
Обозначим ![]() подмножество выделить гиперпараллелепипед
подмножество выделить гиперпараллелепипед ![]() ,
состоящее из значений
,
состоящее из значений ![]() ,
удовлетворяющих условию (3).
,
удовлетворяющих условию (3).
3. Нечеткие ограничения на выходные переменные
![]() ,
(4)
,
(4)
где символы ![]() означают оператор размытия, переводящий четкое множество в приблизительно
равное ему нечеткое.
означают оператор размытия, переводящий четкое множество в приблизительно
равное ему нечеткое.
Согласно уравнению (4) значение ![]() должно находиться приблизительно в диапазоне
должно находиться приблизительно в диапазоне ![]() .
Обозначим
.
Обозначим ![]() подмножество значений
подмножество значений ![]() ,
удовлетворяющих ограничениям (4).
,
удовлетворяющих ограничениям (4).
4. Нечеткие функциональные ограничения
![]() .
(5)
.
(5)
Пространство значений ![]() ,
удовлетворяющих условию (5),образует пространство реакций
,
удовлетворяющих условию (5),образует пространство реакций ![]() .
.
Ограничения (4) и (5) важны в тех случаях,
когда информация о поведении объекта имеет качественный характер. Отображение
ее в количественную форму осуществи с помощью функций принадлежности ![]() .
.
При линейной функции
![]() .
(6)
.
(6)
Функция (6) задается исследователем по
точкам ![]() .
.
В случае экспоненциальной функции
![]() .
(7)
.
(7)
где ![]() - параметр формы кривой,
- параметр формы кривой,
- значение
![]() при котором
при котором ![]() равна
равна .
Функция (7) задается по трем точкам
.
Для гауссовой функции
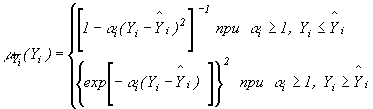 (8)
(8)
![]() .
(9)
.
(9)
где ![]() - параметр формы кривой.
- параметр формы кривой.
Функции (8) и (9) задаются исследователем
точкой, вблизи которой достигается наибольшее значение функции принадлежности ![]() .
.
В случае ![]() - образной функции
- образной функции
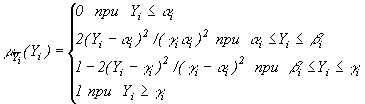 (10)
(10)
где ![]() -
точка перехода
-
точка перехода ![]() .
Функция (10) задается исследователем степенью принадлежности в точках
.
Функция (10) задается исследователем степенью принадлежности в точках ![]() .
.
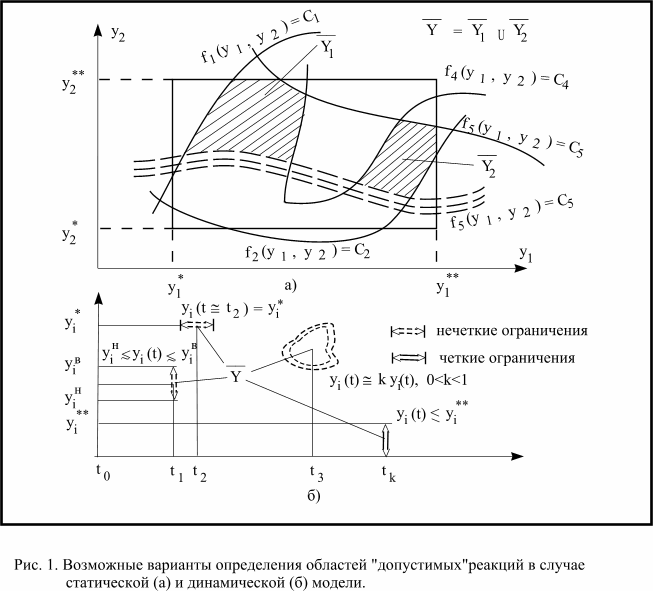
Возможные варианты определения областей “допустимых” реакций модели, то есть реакций, удовлетворяющих ограничениям (2) – (5), приведены на рис.1.
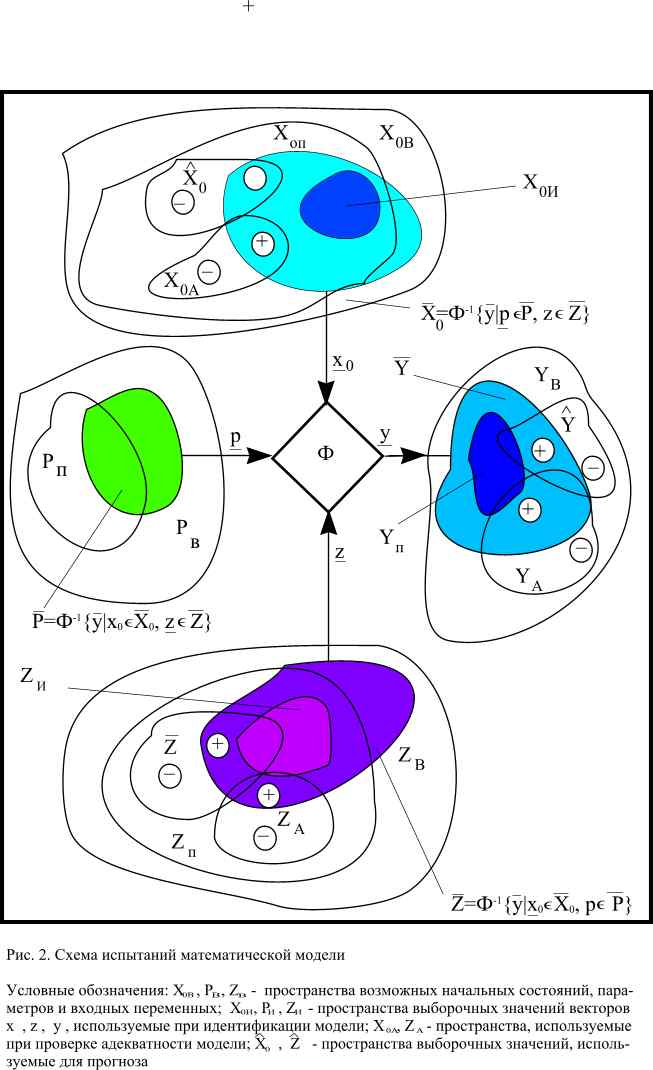
Основываясь на условии (1), выделим сочетания
векторов ![]() ,
где
,
где ![]() .
Каждому из них с помощью оператора
.
Каждому из них с помощью оператора ![]() ставятся в соответствие значения
ставятся в соответствие значения ![]() (см. рис. 2.).
Решение этой задачи важно в двух случаях – когда
(см. рис. 2.).
Решение этой задачи важно в двух случаях – когда ![]() точно неизвестны и когда
точно неизвестны и когда ![]() известны точно, но
известны точно, но ![]() точно неизвестно. Хотя такая задача относится к классу обратных задач,
ее можно решить прямым методом. Для этого установим “правдоподобные” границы
пространств
точно неизвестно. Хотя такая задача относится к классу обратных задач,
ее можно решить прямым методом. Для этого установим “правдоподобные” границы
пространств ![]() (см. рис. 2)
и будем наугад извлекать
(см. рис. 2)
и будем наугад извлекать ![]() сочетания
сочетания ![]() .
Из тех значений, которым с помощью оператора
.
Из тех значений, которым с помощью оператора ![]() ставится в соответствие
ставится в соответствие ![]() ,
образуем пространство
,
образуем пространство ![]() ,
а неудачные сочетания будем отбрасывать.
,
а неудачные сочетания будем отбрасывать.
Итак, предложенная методика состоит в том,
что пространство “допустимых” реакций ![]() ,
сформированное из детерминированных и нечетких ограничений, с помощью обратного
оператора
,
сформированное из детерминированных и нечетких ограничений, с помощью обратного
оператора ![]() отображается в пространство “правдоподобных” значений
отображается в пространство “правдоподобных” значений ![]() в отличие от традиционного подхода, в котором что пространства “допустимых”
значений входных переменных
в отличие от традиционного подхода, в котором что пространства “допустимых”
значений входных переменных ![]() и выходных реакций
и выходных реакций ![]() известны
точно и требуется определить оператор
известны
точно и требуется определить оператор ![]() .
В принципе возможен случай, когда при длительном проведении испытаний модели
и неоднократном расширении границ
.
В принципе возможен случай, когда при длительном проведении испытаний модели
и неоднократном расширении границ ![]() не найдется ни одного сочетания векторов
не найдется ни одного сочетания векторов ![]() ,
отображаемого оператором
,
отображаемого оператором ![]() в
в ![]() . Это
означает, что
. Это
означает, что ![]() неадекватен моделируемому объекту. То же может быть и при испытаниях, в
которых одно или несколько сочетаний
неадекватен моделируемому объекту. То же может быть и при испытаниях, в
которых одно или несколько сочетаний ![]() ,
отображается в
,
отображается в ![]() .
При этом модель будет неустойчивой, так как в результате незначительных
отклонений
.
При этом модель будет неустойчивой, так как в результате незначительных
отклонений ![]() значения вектора
значения вектора ![]() выйдут из пространства его “допустимых” реакций. В подобных ситуациях необходима
коррекция оператора
выйдут из пространства его “допустимых” реакций. В подобных ситуациях необходима
коррекция оператора ![]() .
.
Реализация алгоритма испытаний модели серьезных
затруднений не вызывает. Зная хотя бы приблизительно границы пространств![]() с помощью датчиков случайных чисел можно сгенерировать
с помощью датчиков случайных чисел можно сгенерировать ![]() .
Решение
уравнений с этими значениями позволяет проверить модель и условия выполнения
ограничений. Так как в большинстве случаев плотность вероятности переменных
.
Решение
уравнений с этими значениями позволяет проверить модель и условия выполнения
ограничений. Так как в большинстве случаев плотность вероятности переменных ![]() неизвестна,
то при проведении испытаний используется датчик равномерно распределенных
последовательностей. Достаточно точная оценка числа испытаний может быть
получена с помощью интегральной теоремы Лапласа [7].
неизвестна,
то при проведении испытаний используется датчик равномерно распределенных
последовательностей. Достаточно точная оценка числа испытаний может быть
получена с помощью интегральной теоремы Лапласа [7].
Если модель оказалась неадекватной пространству
“допустимых” реакций, необходима ее коррекция. В этом случае проводят диагностику
результатов статистических испытаний, которая состоит из следующих этапов:
выявление элементов вектора ![]() ,
нарушающих ограничения (2) –(5); выбор параметров модели
,
нарушающих ограничения (2) –(5); выбор параметров модели ![]() ,
от которых зависит
,
от которых зависит ![]() ;
оценка чувствительности
;
оценка чувствительности ![]() к
параметрам
к
параметрам ![]() .
.
Простейший способ коррекции оператора ![]() заключается в замене элементов модели, включающих параметры
заключается в замене элементов модели, включающих параметры ![]() ,
на другие.
,
на другие.
В конечном итоге создается математическая модель, адекватная исследуемому водному объекту, и на ее основе выполняются прогнозы процессов самоочищения воды. Результаты прогнозов можно представить в виде условной плотности вероятности
![]() ,
,
где ![]() - пространство прогнозируемых реакций модели, образуемое при известных
- пространство прогнозируемых реакций модели, образуемое при известных ![]() и множестве значений
и множестве значений ![]() .
.
Применение методики. Предложенная методика была использована для анализа процессов самоочищения воды реки Цны. Данная задача возникла в связи с ухудшением экологической обстановки на участке реки длиной 60 км, начиная от точки сброса очищенных сточных вод с очистных сооружений промышленных сооружений г.Тамбова до гидроузла Троицкой Дубравы.
Гидродинамическая структура потоков в реке чаще всего представляется моделью идеального вытеснения [3]. Однако, для некоторых участков может быть предложена ячеечная модель. Конкретный вид гидродинамической структуры определяется в ходе проведения трассерного эксперимента и решения задачи параметрической идентификации, аналогичной приведенной в работе [7].
В результате анализа существующих типов моделей реки в качестве "кандидата" конструктивной модели предлагаем модель, в которой функциональные зависимости для отдельных процессов взяты из работы [5]:
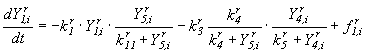 ;
(11)
;
(11)
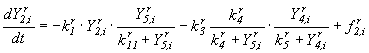 ;
(12)
;
(12)
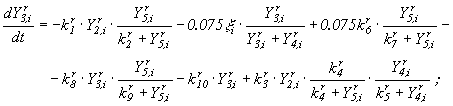 (13)
(13)
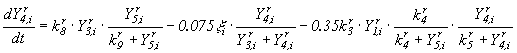 ;
(14)
;
(14)
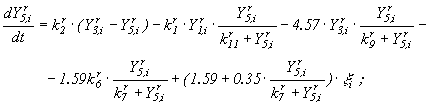 (15)
(15)
![]() (16)
(16)
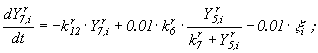 (17)
(17)
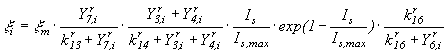 ;
(18)
;
(18)
![]() (19)
(19)
![]() ;
(20)
;
(20)
![]() ;
(21)
;
(21)
![]() ;
(22)
;
(22)
![]() ;
(23)
;
(23)
![]() ;
(24)
;
(24)
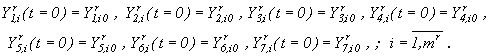 (25)
(25)
Здесь ![]() - концентрация БПК, мг/л;
- концентрация БПК, мг/л;
![]() - концентрация азота органических соединений, мг/л;
- концентрация азота органических соединений, мг/л;
![]() - концентрация аммонийного азота, мг/л;
- концентрация аммонийного азота, мг/л;
![]() - концентрация нитратного азота, мг/л;
- концентрация нитратного азота, мг/л;
![]() - концентрация растворённого кислорода, мг/л;
- концентрация растворённого кислорода, мг/л;
![]() - концентрация ионов шестивалентного хрома, мг/л;
- концентрация ионов шестивалентного хрома, мг/л;
![]() - концентрация общего фосфора, мг/л;
- концентрация общего фосфора, мг/л;
![]() - скорость роста фитопланктона, мг сухого вещества фитопланктона/(л*сутки);
- скорость роста фитопланктона, мг сухого вещества фитопланктона/(л*сутки);
![]() - концентрация насыщения растворённого кислорода, мг/л;
- концентрация насыщения растворённого кислорода, мг/л;
![]() - константа скорости аэробного разложения примесей, 1/сутки;
- константа скорости аэробного разложения примесей, 1/сутки;
![]() - коэффициент реаэрации, 1/сутки;
- коэффициент реаэрации, 1/сутки;
![]() - константа скорости денитрификации, 1/сутки;
- константа скорости денитрификации, 1/сутки;
![]() - константа лимитирования скорости денитрификации концентрацией растворённого
в воде кислорода,
- константа лимитирования скорости денитрификации концентрацией растворённого
в воде кислорода, ![]() ;
;
![]() - константа насыщения по нитратам, мг
- константа насыщения по нитратам, мг ![]() /л;
/л;
![]() - константа скорости отмирания фитопланктона, мг/(л*сутки);
- константа скорости отмирания фитопланктона, мг/(л*сутки);
![]() - константа лимитирования скорости отмирания фитопланктона концентрацией
растворённого кислорода,
- константа лимитирования скорости отмирания фитопланктона концентрацией
растворённого кислорода, ![]() ;
;
![]() - константа скорости нитрификации, 1/сутки;
- константа скорости нитрификации, 1/сутки;
![]() - константа лимитирования скорости нитрификации концентрацией растворённого
кислорода,
- константа лимитирования скорости нитрификации концентрацией растворённого
кислорода, ![]() ;
;
![]() - константа скорости ионного обмена, 1/сутки;
- константа скорости ионного обмена, 1/сутки;
![]() - константа лимитирования скорости аммонификации концентрацией растворённого
кислорода,
- константа лимитирования скорости аммонификации концентрацией растворённого
кислорода, ![]() ;
;
![]() - константа скорости потребления фосфора, 1/сутки;
- константа скорости потребления фосфора, 1/сутки;
![]() - константа лимитирования роста фитопланктона концентрацией фосфора, мг/л;
- константа лимитирования роста фитопланктона концентрацией фосфора, мг/л;
![]() - константа лимитирования скорости роста фитопланктона концентрацией аммонийного
азота, мг/л;
- константа лимитирования скорости роста фитопланктона концентрацией аммонийного
азота, мг/л;
![]() - константа скорости поглощения ионов тяжёлых металлов, 1/сутки;
- константа скорости поглощения ионов тяжёлых металлов, 1/сутки;
![]() -константа
ингибирования скорости роста фитопланктона концентрацией ионов шестивалентного
хрома, мг/л;
-константа
ингибирования скорости роста фитопланктона концентрацией ионов шестивалентного
хрома, мг/л;
![]() - максимальное и текущее в данной местности, в данный период времени
- максимальное и текущее в данной местности, в данный период времени
года значение интенсивности солнечной радиации, лм/сутки;
![]() - соответственно, функция целой части числа и единичная функция;
- соответственно, функция целой части числа и единичная функция;
![]() - соответственно, время восхода и продолжительность светового дня, час;
- соответственно, время восхода и продолжительность светового дня, час;
![]() - максимум скорости роста фитопланктона, мг сухого вещества
- максимум скорости роста фитопланктона, мг сухого вещества
фитопланктона/(л*сутки);
![]() - время, сутки;
- время, сутки;
![]() - температура воды, град С;
- температура воды, град С;
![]() - световое время суток, час;
- световое время суток, час;
![]() - скорость поступления органических веществ с берега, мг/(л*сутки);
- скорость поступления органических веществ с берега, мг/(л*сутки);
![]() - скорость поступления азота органических веществ с берега, мг/(л*сутки);
- скорость поступления азота органических веществ с берега, мг/(л*сутки);
![]() - время, в течение которого происходит смыв органики с полей, сутки;
- время, в течение которого происходит смыв органики с полей, сутки;
![]() - номер участка реки;
- номер участка реки;
![]() - начальные условия для
- начальные условия для ![]() на
на ![]() - ом
участке реки, мг/л;
- ом
участке реки, мг/л;
![]() - число участков с относительно постоянными гидрохимическими параметрами.
Значения стехиометрических коэффициентов взяты из литературы (9): 0.075
- количество азота в мг, содержащееся в 1 кг сухого веса растений; 0.35
- коэффициент эквивалентного превращения кислорода в нитритный азот; 1.59
- количество кислорода в мг, содержащееся в 1 кг сухого
веса
растений (высвобождение азота растений предполагается в аммонийной форме);
4.57 - количество кислорода в мг, потребляемое при аэробном окислении 1
мг аммонийного азота; 0.01 - количество фосфора, содержащееся в 1 мг сухого
веса фитопланктона; 0.02 –значение
- число участков с относительно постоянными гидрохимическими параметрами.
Значения стехиометрических коэффициентов взяты из литературы (9): 0.075
- количество азота в мг, содержащееся в 1 кг сухого веса растений; 0.35
- коэффициент эквивалентного превращения кислорода в нитритный азот; 1.59
- количество кислорода в мг, содержащееся в 1 кг сухого
веса
растений (высвобождение азота растений предполагается в аммонийной форме);
4.57 - количество кислорода в мг, потребляемое при аэробном окислении 1
мг аммонийного азота; 0.01 - количество фосфора, содержащееся в 1 мг сухого
веса фитопланктона; 0.02 –значение ![]() при 20 град С.
при 20 град С.
Если в исследуемом водоёме отсутствуют те или иные процессы, то соответствующие составляющие, описывающие данные процессы в математической модели (11) - (25) должны быть исключены из неё.
Анализ процессов самоочищения воды реки
проводился на участке реки длиной 60 км, начиная от точки сброса очищенных
сточных вод с очистных сооружений П/О “Пигмент” до Троицко – Дубравского
гидроузла
( см. рис.3.). Река Цна
по классификации Огиевского относится к 3-й категории и имеет хозяйственно
– питьевое назначение. Для исследуемого участка характерно следующее: среднегодовой
расход – 12,3 м3/с , русло
умеренно извилистое шириной 45-60 м, песчано-илистое, деформирующееся,
незначительно заросшее водной растительностью. Прилагаемая местность –
наклонная равнина, по левобережью открытая, по правобережью поросшая лесом.
По берегам реки расположены населенные пункты, местные водозаборы, садово-огородные
общества, использующие воду, зоны отдыха трудящихся. В связи с тем, что
на участке имеются два гидроузла и несколько притоков, при моделировании
разобьем его на 6 участков с относительно постоянными гидрохимическими
параметрами. Схематично они изображены на рис.3.
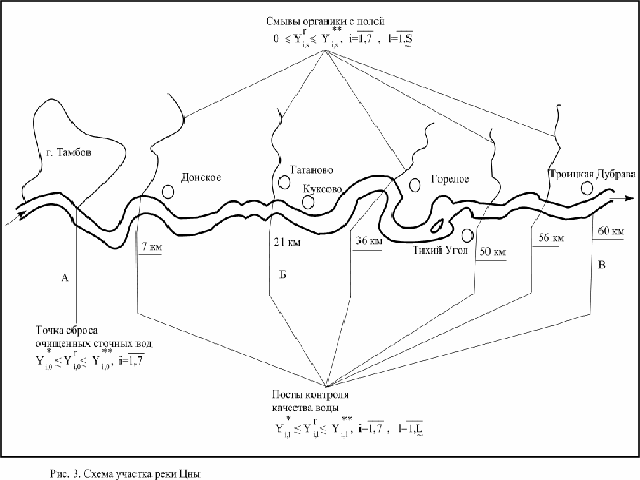
В результате исследования процессов, протекающих в реке, были выделены процессы аэробного окисления органики, нитрификации, де нитрификации, роста и отмирания планктона, деаэрации воды кислородом воздуха, аммонификации белка и мочевины, ионного обмена и другие. В качестве “кандидата” модели для проведения имитационного испытания использована модель (11)-(25).
Формирование ограничений на выходные переменные
модели вида (2)-(5) и определение диапазонов изменения начальных состояний
и внешних воздействий ( смывы органики с полей ) осуществлялось на основе
информации Центрально – Черноземной региональной, городской и заводской
( А/О “Пигмент”) гидрохимических лабораторий с учетом полевых измерений
концентраций аммонийного и нитратного азота, а также растворенного кислорода
в сечениях А, Б, В, выполненных с помощью передвижной лаборатории контроля
качества поверхностных вод. В тех случаях, когда информация носила качественный
характер, ее преобразование в количественную форму осуществлялось с помощью
формул (6) – (10). Часть ограничений (2) – (5) проиллюстрирована на
рис.3 и рис.4.
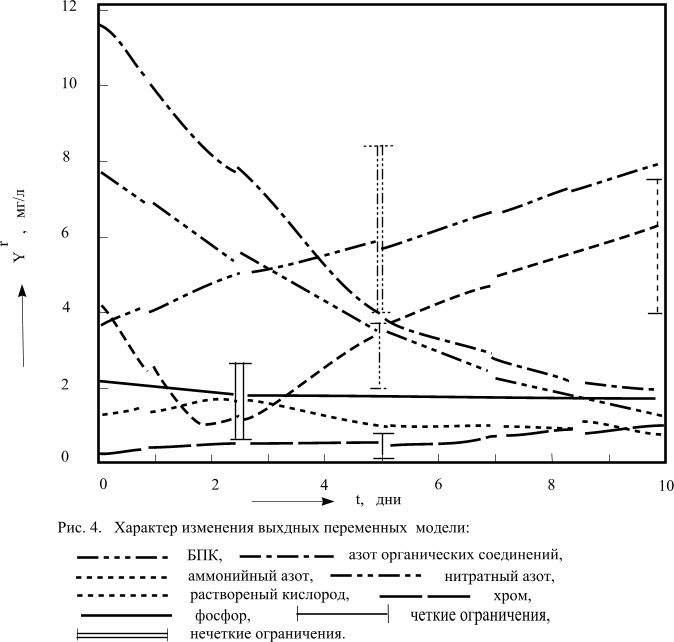
При решении системы уравнений модели в
ходе имитационного испытания суммарный интервал времени для всего участка
длиной 60 км составил 10 дней. Значения коэффициентов модели выбирались
из диапазонов их “правдоподобных” значений. На
рис.5(а) начальные
диапазоны изменения коэффициентов отмечены под числовой осью. Характер
изменения выходных переменных при определенных значениях коэффициентов
и начальных условий (см. табл. 1) приведен на рис.4. При отыскании
“правдоподобных” диапазонов коэффициентов было выполнено несколько пробных
серий решений системы уравнений. На рис. 5(а) для коэффициента
штриховкой под числовой осью отмечен “правдоподобный” диапазон. “Допустимые”
реакции с значениями в пределах него образуют пустое множество.
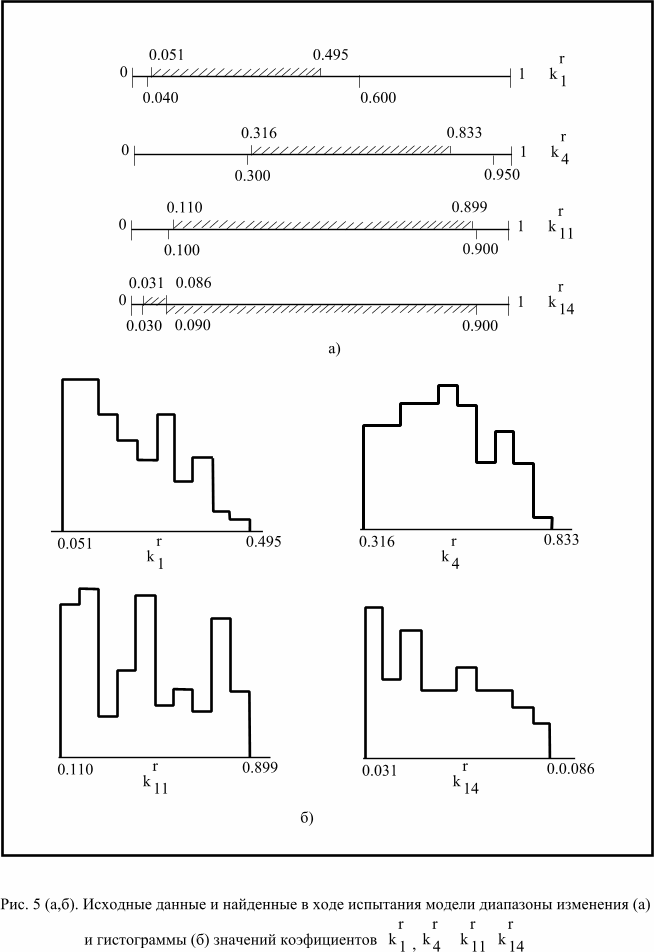
Для окончательного выяснения диапазонов
изменения коэффициентов было проведено 9300 решений системы уравнений,
в 10 % из них получены решения, удовлетворяющие ограничениям. В табл. 1
приведены диапазоны изменения всех коэффициентов модели, а на
рис.5 (а) – коэффициентов,показанные штриховкой над числовой осью. Из этого рисунка видно, что для
одних коэффициентов “допустимые” реакции получены во всем предполагаемом
диапазоне, для других – он был назначен с большим “запасом”.
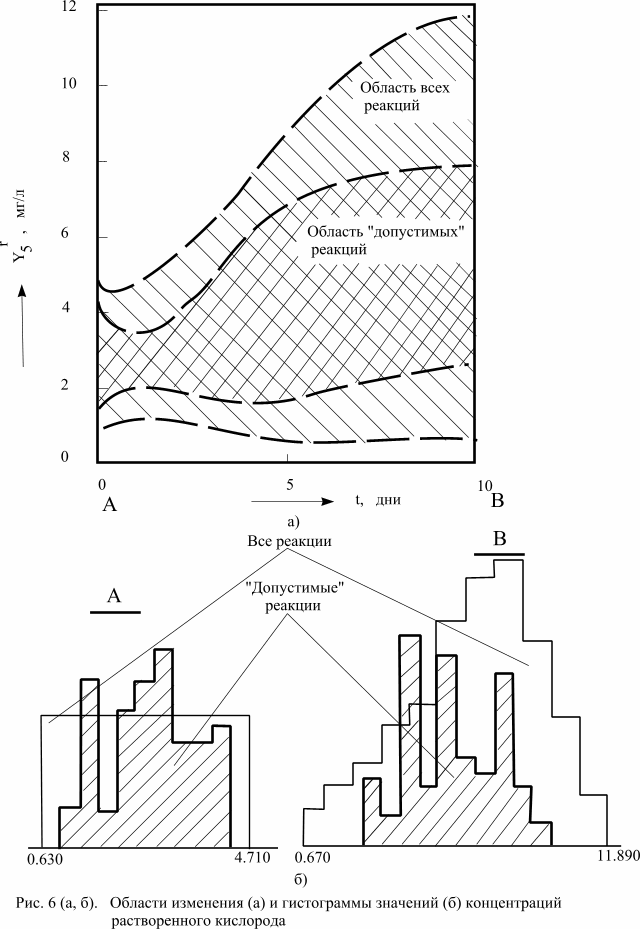
Все семейство кривых изменения во времени образует некоторую область. На рис.6 изображены области изменения концентраций растворенного кислорода для всех реакций модели и реакций, удовлетворяющих ограничениям, а также гистограммы на рис.5 (б) показаны гистограммы значений отдельных коэффициентов для “допустимых” реакций модели.
Диапазоны изменения всех коэффициентов
модели. Таблица 1.
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
![]() (1)
(1)
где ![]() - некоторый функциональный оператор, отображающий пространства всех начальных
состояний объекта
- некоторый функциональный оператор, отображающий пространства всех начальных
состояний объекта ![]() , параметров
, параметров ![]() и независимых входных переменных
и независимых входных переменных ![]() ,
реализованных на интервале времени
,
реализованных на интервале времени ![]() в пространство выходных переменных
в пространство выходных переменных ![]() .
.
Имеющуюся количественную и качественную информацию о поведении объекта представим следующим образом:
1. Детерминированные ограничения на выходные переменные модели
![]() (2)
(2)
В результате ограничений (2) в пространстве
реакций можно выделить гиперпараллелепипед ![]() ,
объем которого
,
объем которого
![]()
2. Функциональные ограничения
![]() ,
(3)
,
(3)
где ![]() - некоторые функции от
- некоторые функции от ![]() ,
заданные в явном или неявном виде.
,
заданные в явном или неявном виде.
Обозначим ![]() подмножество выделить гиперпараллелепипед
подмножество выделить гиперпараллелепипед ![]() ,
состоящее из значений
,
состоящее из значений ![]() ,
удовлетворяющих условию (3).
,
удовлетворяющих условию (3).
3. Нечеткие ограничения на выходные переменные
![]() ,
(4)
,
(4)
где символы ![]() означают оператор размытия, переводящий четкое множество в приблизительно
равное ему нечеткое.
означают оператор размытия, переводящий четкое множество в приблизительно
равное ему нечеткое.
Согласно уравнению (4) значение ![]() должно находиться приблизительно в диапазоне
должно находиться приблизительно в диапазоне ![]() .
Обозначим
.
Обозначим ![]() подмножество значений
подмножество значений ![]() ,
удовлетворяющих ограничениям (4).
,
удовлетворяющих ограничениям (4).
4. Нечеткие функциональные ограничения
![]() .
(5)
.
(5)
Пространство значений ![]() ,
удовлетворяющих условию (5),образует пространство реакций
,
удовлетворяющих условию (5),образует пространство реакций ![]() .
.
Ограничения (4) и (5) важны в тех случаях,
когда информация о поведении объекта имеет качественный характер. Отображение
ее в количественную форму осуществи с помощью функций принадлежности ![]() .
.
При линейной функции
![]() .
(6)
.
(6)
Функция (6) задается исследователем по
точкам ![]() .
.
В случае экспоненциальной функции
![]() .
(7)
.
(7)
где ![]() - параметр формы кривой,
- параметр формы кривой,
- значение
![]() при котором
при котором ![]() равна
равна .
Функция (7) задается по трем точкам
.
Для гауссовой функции
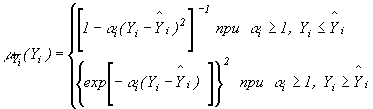 (8)
(8)
![]() .
(9)
.
(9)
где ![]() - параметр формы кривой.
- параметр формы кривой.
Функции (8) и (9) задаются исследователем
точкой, вблизи которой достигается наибольшее значение функции принадлежности ![]() .
.
В случае ![]() - образной функции
- образной функции
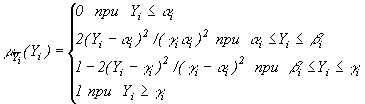 (10)
(10)
где ![]() -
точка перехода
-
точка перехода ![]() .
Функция (10) задается исследователем степенью принадлежности в точках
.
Функция (10) задается исследователем степенью принадлежности в точках ![]() .
.
Возможные варианты определения областей “допустимых” реакций модели, то есть реакций, удовлетворяющих ограничениям (2) – (5), приведены на рис. 1.
Основываясь на условии (1), выделим сочетания
векторов ![]() ,
где
,
где ![]() .
Каждому из них с помощью оператора
.
Каждому из них с помощью оператора ![]() ставятся в соответствие значения
ставятся в соответствие значения ![]() (см. рис. 2.).
Решение этой задачи важно в двух случаях – когда
(см. рис. 2.).
Решение этой задачи важно в двух случаях – когда ![]() точно неизвестны и когда
точно неизвестны и когда ![]() известны точно, но
известны точно, но ![]() точно неизвестно. Хотя такая задача относится к классу обратных задач,
ее можно решить прямым методом. Для этого установим “правдоподобные” границы
пространств
точно неизвестно. Хотя такая задача относится к классу обратных задач,
ее можно решить прямым методом. Для этого установим “правдоподобные” границы
пространств ![]() (см.рис. 2)
и будем наугад извлекать
(см.рис. 2)
и будем наугад извлекать ![]() сочетания
сочетания ![]() .
Из тех значений, которым с помощью оператора
.
Из тех значений, которым с помощью оператора ![]() ставится в соответствие
ставится в соответствие ![]() ,
образуем пространство
,
образуем пространство ![]() ,
а неудачные сочетания будем отбрасывать.
,
а неудачные сочетания будем отбрасывать.
Итак, предложенная методика состоит в том,
что пространство “допустимых” реакций ![]() ,
сформированное из детерминированных и нечетких ограничений, с помощью обратного
оператора
,
сформированное из детерминированных и нечетких ограничений, с помощью обратного
оператора ![]() отображается в пространство “правдоподобных” значений
отображается в пространство “правдоподобных” значений ![]() в отличие от традиционного подхода, в котором что пространства “допустимых”
значений входных переменных
в отличие от традиционного подхода, в котором что пространства “допустимых”
значений входных переменных ![]() и выходных реакций
и выходных реакций ![]() известны
точно и требуется определить оператор
известны
точно и требуется определить оператор ![]() .
В принципе возможен случай, когда при длительном проведении испытаний модели
и неоднократном расширении границ
.
В принципе возможен случай, когда при длительном проведении испытаний модели
и неоднократном расширении границ ![]() не найдется ни одного сочетания векторов
не найдется ни одного сочетания векторов ![]() ,
отображаемого оператором
,
отображаемого оператором ![]() в
в ![]() . Это
означает, что
. Это
означает, что ![]() неадекватен моделируемому объекту. То же может быть и при испытаниях, в
которых одно или несколько сочетаний
неадекватен моделируемому объекту. То же может быть и при испытаниях, в
которых одно или несколько сочетаний ![]() ,
отображается в
,
отображается в ![]() .
При этом модель будет неустойчивой, так как в результате незначительных
отклонений
.
При этом модель будет неустойчивой, так как в результате незначительных
отклонений ![]() значения вектора
значения вектора ![]() выйдут из пространства его “допустимых” реакций. В подобных ситуациях необходима
коррекция оператора
выйдут из пространства его “допустимых” реакций. В подобных ситуациях необходима
коррекция оператора ![]() .
.
Реализация алгоритма испытаний модели серьезных
затруднений не вызывает. Зная хотя бы приблизительно границы пространств![]() с помощью датчиков случайных чисел можно сгенерировать
с помощью датчиков случайных чисел можно сгенерировать ![]() .
Решение
уравнений с этими значениями позволяет проверить модель и условия выполнения
ограничений. Так как в большинстве случаев плотность вероятности переменных
.
Решение
уравнений с этими значениями позволяет проверить модель и условия выполнения
ограничений. Так как в большинстве случаев плотность вероятности переменных ![]() неизвестна,
то при проведении испытаний используется датчик равномерно распределенных
последовательностей. Достаточно точная оценка числа испытаний может быть
получена с помощью интегральной теоремы Лапласа [7].
неизвестна,
то при проведении испытаний используется датчик равномерно распределенных
последовательностей. Достаточно точная оценка числа испытаний может быть
получена с помощью интегральной теоремы Лапласа [7].
Если модель оказалась неадекватной пространству
“допустимых” реакций, необходима ее коррекция. В этом случае проводят диагностику
результатов статистических испытаний, которая состоит из следующих этапов:
выявление элементов вектора ![]() ,
нарушающих ограничения (2) –(5); выбор параметров модели
,
нарушающих ограничения (2) –(5); выбор параметров модели ![]() ,
от которых зависит
,
от которых зависит ![]() ;
оценка чувствительности
;
оценка чувствительности ![]() к
параметрам
к
параметрам ![]() .
.
Простейший способ коррекции оператора ![]() заключается в замене элементов модели, включающих параметры
заключается в замене элементов модели, включающих параметры ![]() ,
на другие.
,
на другие.
В конечном итоге создается математическая модель, адекватная исследуемому водному объекту, и на ее основе выполняются прогнозы процессов самоочищения воды. Результаты прогнозов можно представить в виде условной плотности вероятности
![]() ,
,
где ![]() - пространство прогнозируемых реакций модели, образуемое при известных
- пространство прогнозируемых реакций модели, образуемое при известных ![]() и множестве значений
и множестве значений ![]() .
.
Применение методики. Предложенная методика была использована для анализа процессов самоочищения воды реки Цны. Данная задача возникла в связи с ухудшением экологической обстановки на участке реки длиной 60 км, начиная от точки сброса очищенных сточных вод с очистных сооружений промышленных сооружений г.Тамбова до гидроузла Троицкой Дубравы.
Гидродинамическая структура потоков в реке чаще всего представляется моделью идеального вытеснения [3]. Однако, для некоторых участков может быть предложена ячеечная модель. Конкретный вид гидродинамической структуры определяется в ходе проведения трассерного эксперимента и решения задачи параметрической идентификации, аналогичной приведенной в работе [7].
В результате анализа существующих типов моделей реки в качестве "кандидата" конструктивной модели предлагаем модель, в которой функциональные зависимости для отдельных процессов взяты из работы [5]:
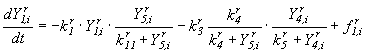 ;
(11)
;
(11)
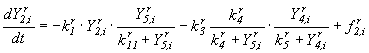 ;
(12)
;
(12)
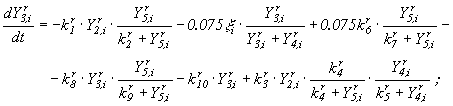 (13)
(13)
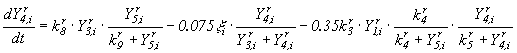 ;
(14)
;
(14)
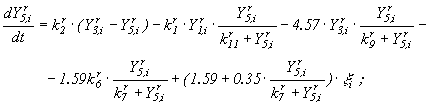 (15)
(15)
![]() (16)
(16)
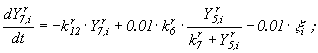 (17)
(17)
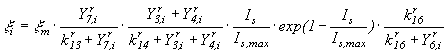 ;
(18)
;
(18)
![]() (19)
(19)
![]() ;
(20)
;
(20)
![]() ;
(21)
;
(21)
![]() ;
(22)
;
(22)
![]() ;
(23)
;
(23)
![]() ;
(24)
;
(24)
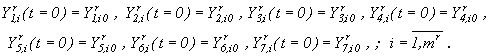 (25)
(25)
Здесь ![]() - концентрация БПК, мг/л;
- концентрация БПК, мг/л;
![]() - концентрация азота органических соединений, мг/л;
- концентрация азота органических соединений, мг/л;
![]() - концентрация аммонийного азота, мг/л;
- концентрация аммонийного азота, мг/л;
![]() - концентрация нитратного азота, мг/л;
- концентрация нитратного азота, мг/л;
![]() - концентрация растворённого кислорода, мг/л;
- концентрация растворённого кислорода, мг/л;
![]() - концентрация ионов шестивалентного хрома, мг/л;
- концентрация ионов шестивалентного хрома, мг/л;
![]() - концентрация общего фосфора, мг/л;
- концентрация общего фосфора, мг/л;
![]() - скорость роста фитопланктона, мг сухого вещества фитопланктона/(л*сутки);
- скорость роста фитопланктона, мг сухого вещества фитопланктона/(л*сутки);
![]() - концентрация насыщения растворённого кислорода, мг/л;
- концентрация насыщения растворённого кислорода, мг/л;
![]() - константа скорости аэробного разложения примесей, 1/сутки;
- константа скорости аэробного разложения примесей, 1/сутки;
![]() - коэффициент реаэрации, 1/сутки;
- коэффициент реаэрации, 1/сутки;
![]() - константа скорости денитрификации, 1/сутки;
- константа скорости денитрификации, 1/сутки;
![]() - константа лимитирования скорости денитрификации концентрацией растворённого
в воде кислорода,
- константа лимитирования скорости денитрификации концентрацией растворённого
в воде кислорода, ![]() ;
;
![]() - константа насыщения по нитратам, мг
- константа насыщения по нитратам, мг ![]() /л;
/л;
![]() - константа скорости отмирания фитопланктона, мг/(л*сутки);
- константа скорости отмирания фитопланктона, мг/(л*сутки);
![]() - константа лимитирования скорости отмирания фитопланктона концентрацией
растворённого кислорода,
- константа лимитирования скорости отмирания фитопланктона концентрацией
растворённого кислорода, ![]() ;
;
![]() - константа скорости нитрификации, 1/сутки;
- константа скорости нитрификации, 1/сутки;
![]() - константа лимитирования скорости нитрификации концентрацией растворённого
кислорода,
- константа лимитирования скорости нитрификации концентрацией растворённого
кислорода, ![]() ;
;
![]() - константа скорости ионного обмена, 1/сутки;
- константа скорости ионного обмена, 1/сутки;
![]() - константа лимитирования скорости аммонификации концентрацией растворённого
кислорода,
- константа лимитирования скорости аммонификации концентрацией растворённого
кислорода, ![]() ;
;
![]() - константа скорости потребления фосфора, 1/сутки;
- константа скорости потребления фосфора, 1/сутки;
![]() - константа лимитирования роста фитопланктона концентрацией фосфора, мг/л;
- константа лимитирования роста фитопланктона концентрацией фосфора, мг/л;
![]() - константа лимитирования скорости роста фитопланктона концентрацией аммонийного
азота, мг/л;
- константа лимитирования скорости роста фитопланктона концентрацией аммонийного
азота, мг/л;
![]() - константа скорости поглощения ионов тяжёлых металлов, 1/сутки;
- константа скорости поглощения ионов тяжёлых металлов, 1/сутки;
![]() -константа
ингибирования скорости роста фитопланктона концентрацией ионов шестивалентного
хрома, мг/л;
-константа
ингибирования скорости роста фитопланктона концентрацией ионов шестивалентного
хрома, мг/л;
![]() - максимальное и текущее в данной местности, в данный период времени
- максимальное и текущее в данной местности, в данный период времени
года значение интенсивности солнечной радиации, лм/сутки;
![]() - соответственно, функция целой части числа и единичная функция;
- соответственно, функция целой части числа и единичная функция;
![]() - соответственно, время восхода и продолжительность светового дня, час;
- соответственно, время восхода и продолжительность светового дня, час;
![]() - максимум скорости роста фитопланктона, мг сухого вещества
- максимум скорости роста фитопланктона, мг сухого вещества
фитопланктона/(л*сутки);
![]() - время, сутки;
- время, сутки;
![]() - температура воды, град С;
- температура воды, град С;
![]() - световое время суток, час;
- световое время суток, час;
![]() - скорость поступления органических веществ с берега, мг/(л*сутки);
- скорость поступления органических веществ с берега, мг/(л*сутки);
![]() - скорость поступления азота органических веществ с берега, мг/(л*сутки);
- скорость поступления азота органических веществ с берега, мг/(л*сутки);
![]() - время, в течение которого происходит смыв органики с полей, сутки;
- время, в течение которого происходит смыв органики с полей, сутки;
![]() - номер участка реки;
- номер участка реки;
![]() - начальные условия для
- начальные условия для ![]() на
на ![]() - ом
участке реки, мг/л;
- ом
участке реки, мг/л;
![]() - число участков с относительно постоянными гидрохимическими параметрами.
Значения стехиометрических коэффициентов взяты из литературы (9): 0.075
- количество азота в мг, содержащееся в 1 кг сухого веса растений; 0.35
- коэффициент эквивалентного превращения кислорода в нитритный азот; 1.59
- количество кислорода в мг, содержащееся в 1 кг сухого
веса
растений (высвобождение азота растений предполагается в аммонийной форме);
4.57 - количество кислорода в мг, потребляемое при аэробном окислении 1
мг аммонийного азота; 0.01 - количество фосфора, содержащееся в 1 мг сухого
веса фитопланктона; 0.02 –значение
- число участков с относительно постоянными гидрохимическими параметрами.
Значения стехиометрических коэффициентов взяты из литературы (9): 0.075
- количество азота в мг, содержащееся в 1 кг сухого веса растений; 0.35
- коэффициент эквивалентного превращения кислорода в нитритный азот; 1.59
- количество кислорода в мг, содержащееся в 1 кг сухого
веса
растений (высвобождение азота растений предполагается в аммонийной форме);
4.57 - количество кислорода в мг, потребляемое при аэробном окислении 1
мг аммонийного азота; 0.01 - количество фосфора, содержащееся в 1 мг сухого
веса фитопланктона; 0.02 –значение ![]() при 20 град С.
при 20 град С.
Если в исследуемом водоёме отсутствуют те или иные процессы, то соответствующие составляющие, описывающие данные процессы в математической модели (11) - (25) должны быть исключены из неё.
Анализ процессов самоочищения воды реки проводился на участке реки длиной 60 км, начиная от точки сброса очищенных сточных вод с очистных сооружений П/О “Пигмент” до Троицко – Дубравского гидроузла ( см. рис.3.). Река Цна по классификации Огиевского относится к 3-й категории и имеет хозяйственно – питьевое назначение. Для исследуемого участка характерно следующее: среднегодовой расход – 12,3 м3/с , русло умеренно извилистое шириной 45-60 м, песчано-илистое, деформирующееся, незначительно заросшее водной растительностью. Прилагаемая местность – наклонная равнина, по левобережью открытая, по правобережью поросшая лесом. По берегам реки расположены населенные пункты, местные водозаборы, садово-огородные общества, использующие воду, зоны отдыха трудящихся. В связи с тем, что на участке имеются два гидроузла и несколько притоков, при моделировании разобьем его на 6 участков с относительно постоянными гидрохимическими параметрами. Схематично они изображены на рис.3.
В результате исследования процессов, протекающих в реке, были выделены процессы аэробного окисления органики, нитрификации, де нитрификации, роста и отмирания планктона, деаэрации воды кислородом воздуха, аммонификации белка и мочевины, ионного обмена и другие. В качестве “кандидата” модели для проведения имитационного испытания использована модель (11)-(25).
Формирование ограничений на выходные переменные модели вида (2)-(5) и определение диапазонов изменения начальных состояний и внешних воздействий ( смывы органики с полей ) осуществлялось на основе информации Центрально – Черноземной региональной, городской и заводской ( А/О “Пигмент”) гидрохимических лабораторий с учетом полевых измерений концентраций аммонийного и нитратного азота, а также растворенного кислорода в сечениях А, Б, В, выполненных с помощью передвижной лаборатории контроля качества поверхностных вод. В тех случаях, когда информация носила качественный характер, ее преобразование в количественную форму осуществлялось с помощью формул (6) – (10). Часть ограничений (2) – (5) проиллюстрирована на рис.3 и рис.4.
При решении системы уравнений модели в ходе имитационного испытания суммарный интервал времени для всего участка длиной 60 км составил 10 дней. Значения коэффициентов модели выбирались из диапазонов их “правдоподобных” значений. На рис.5(а) начальные диапазоны изменения коэффициентов отмечены под числовой осью. Характер изменения выходных переменных при определенных значениях коэффициентов и начальных условий (см. табл. 1) приведен на рис.4. При отыскании “правдоподобных” диапазонов коэффициентов было выполнено несколько пробных серий решений системы уравнений. На рис.5(а) для коэффициента штриховкой под числовой осью отмечен “правдоподобный” диапазон. “Допустимые” реакции с значениями в пределах него образуют пустое множество.
Для окончательного выяснения диапазонов изменения коэффициентов было проведено 9300 решений системы уравнений, в 10 % из них получены решения, удовлетворяющие ограничениям. В табл. 1 приведены диапазоны изменения всех коэффициентов модели, а на рис.5 (а) – коэффициентов, показанные штриховкой над числовой осью. Из этого рисунка видно, что для одних коэффициентов “допустимые” реакции получены во всем предполагаемом диапазоне, для других – он был назначен с большим “запасом”.
Все семейство кривых изменения во времени образует некоторую область. На рис.6 изображены области изменения концентраций растворенного кислорода для всех реакций модели и реакций, удовлетворяющих ограничениям, а также гистограммы на рис.5 (б) показаны гистограммы значений отдельных коэффициентов для “допустимых” реакций модели.
Диапазоны изменения всех коэффициентов
модели. Таблица 1.
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
В случаях, когда при заданных диапазонах изменения коэффициентов образуется пустое множество “допустимых” реакций, их коррекция осуществляется на основе анализа чувствительности выходных переменных к изменению коэффициентов модели.
В результате проведения имитационного испытания была создана математическая модель исследуемого участка реки Цны, удовлетворяющая всем имеющимся экспериментальным данным. Затраты машинного времени на идентификацию модели с быстродействием ПЭВМ 106 оп/с составили менее двух часов. Для проверки адекватности в июне 1990 года были проведены расчеты по модели и полевые измерения состояния качества воды ( концентраций органического, нитратного, аммонийного азота, растворенного кислорода) в сечениях А, Б, В участка реки. Оказалось, что все концентрации, рассчитанные по модели, попадают в 95 % доверительный интервал. При этом максимальная относительная ошибка по нитратному, аммонийному азоту и растворенному кислороду не превышает 10 %, органическому азоту – 15.8 %.
На заключительном этапе исследования участка реки Цны были выполнены прогнозы содержания в воде растворенного кислорода и примесей в зависимости от степени очистки стоков в сечении А, на основе следующего правила:
если
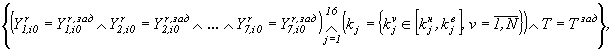
то
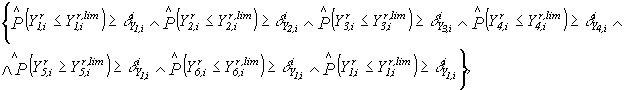
где ![]() - концентрации примесей , растворенного кислорода и температура в
- концентрации примесей , растворенного кислорода и температура в ![]() - ом створе реки, известные в момент прогноза
- ом створе реки, известные в момент прогноза ![]() ;
;
![]() - нижняя и верхняя границы изменения коэффициента
- нижняя и верхняя границы изменения коэффициента ![]() ;
;
![]() - вероятность;
- вероятность;
![]() - предельно допустимые значения концентраций веществ в речном в потоке;
- предельно допустимые значения концентраций веществ в речном в потоке;
![]() - расчетные значения вероятностей;
- расчетные значения вероятностей;
![]() - количество случайных значений коэффициента
- количество случайных значений коэффициента ![]() .
.
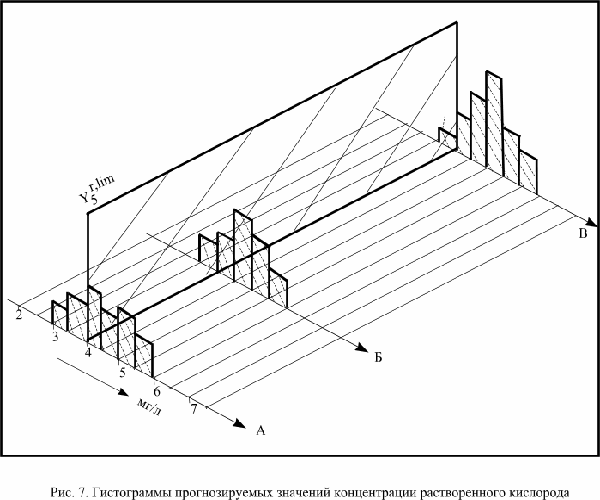
Гистограммы прогнозируемых концентраций
растворенного в воде кислорода приведены на
рис.7.
Предложенная методика моделирования была
использована для решения задачи оптимизации режимов работы локальных очистных
сооружений промышленных предприятий г.Тамбова.
2. Математические модели контроля загрязнения воды / Под редакцией А. Джеймса. М.: Мир, 1981.
3. Попов Н.С., Бодров В.И., Перов В.П. // Химическая промышленность за рубежом. 1984. № 1. С.28
4. Родзиллер И.Д. Прогноз качества воды водоемов – приемников сточных вод. М.: Стройиздат , 1984.
5. Bedford K.W., Sykes R.M., Libiski C. // J. of Env. Eng. 1983. V. 109. No 3. P. 535.
6. Нечеткие множества и теория возможностей . Последние достижения / Под редакцией Р. Ягера М.: Радио и связь. 1986.
7. Попов Н.С. Немтинов В.А. Мокрозуб В.Г. Методика автоматизированного моделирования процессов самоочищения реки с малым расходом воды в условиях неопределенности // Химическая промышленность, 1992. № 9. С 545.
8. Кузин В.Д. Основы кибернетики. М.: Энергия , 1973. Т.2.
9. Jorgensen S.E. // Modeling Identification and Control in Environmental Systems; North-Holland Publ. Comp. 1978. P. 473.
|
|
|
|